Master The Art Of Parabolas: Vertex, Focus, And Directrix Unveiled

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Parabolas, with their gracefully curved shapes, have intrigued mathematicians and artists alike for centuries. These elegantly simple yet profoundly complex curves play a crucial role in various fields, from mathematics and physics to engineering and architecture. Understanding the intricacies of parabolas, including their vertex, focus, and directrix, is not only intellectually stimulating but also practical in solving real-world problems.

In this comprehensive guide, we will delve into the captivating world of parabolas, unraveling their mysteries and mastering the art of working with these fascinating curves. Whether you're a student striving to grasp the fundamental concepts of parabolas or a professional seeking to apply their principles in practical applications, this exploration will equip you with the knowledge and skills to navigate the enchanting realm of parabolas with confidence and expertise.

Throughout this journey, we will demystify the essential components of parabolas, shedding light on their defining characteristics and illuminating the relationships between their various elements. By the end of this exploration, you will not only comprehend the significance of the vertex, focus, and directrix of a parabola but also appreciate the profound beauty and elegance inherent in these mathematical constructs.

So, fasten your seatbelts and get ready to embark on an exhilarating expedition into the captivating world of parabolas. Whether you're a math enthusiast, a curious learner, or simply someone fascinated by the wonders of mathematics, this exploration promises to unravel the enigmatic allure of parabolas and empower you to wield their mathematical prowess with finesse and proficiency. Let's dive in and unravel the secrets of parabolas, one curve at a time.

Understanding Parabolas

Parabolas, the graceful curves that adorn the realm of mathematics, are a fundamental shape that arises from the quadratic functions. These curves possess a symmetrical, U-shaped form that has captivated mathematicians, scientists, and artists for centuries. Understanding the essence of parabolas involves unraveling their defining characteristics and recognizing their omnipresence in the natural world and human-made structures.

At its core, a parabola is defined as the set of all points that are equidistant from a fixed point, known as the focus, and a fixed line, known as the directrix. This elegant definition encapsulates the essence of parabolas, illuminating their geometric significance and mathematical elegance. Whether it's the trajectory of a projectile, the reflective properties of a satellite dish, or the graceful arcs of architectural marvels, parabolas manifest in diverse domains, underscoring their universal relevance and practical applications.

In the realm of algebra, parabolas are closely linked to quadratic equations, with their standard form represented as y = ax^2 + bx + c. This canonical form encapsulates the essential attributes of a parabola, including its vertex, axis of symmetry, and the direction of its opening. By manipulating the coefficients a, b, and c, mathematicians and scientists can transform and analyze parabolic curves, unlocking valuable insights into their behavior and properties.

Moreover, parabolas exhibit a remarkable symmetry, with their axis serving as a line of reflection that partitions the curve into two identical halves. This inherent symmetry not only underscores the aesthetic appeal of parabolas but also facilitates their analysis and comprehension, enabling mathematicians to discern patterns, relationships, and trends embedded within these captivating curves.

In the natural world, parabolic shapes abound, from the trajectory of a thrown ball to the graceful arcs of fountains and the intricate designs of suspension bridges. The ubiquity of parabolas underscores their intrinsic connection to the dynamics of motion, the principles of optics, and the structural integrity of architectural marvels, highlighting their indispensable role in shaping the fabric of our physical reality.

By grasping the foundational principles of parabolas, individuals gain a profound appreciation for the elegance and utility of these captivating curves, empowering them to perceive the world through a mathematical lens and harness the power of parabolas to solve complex problems, unravel scientific phenomena, and appreciate the inherent beauty of mathematical constructs.

The Vertex of a Parabola

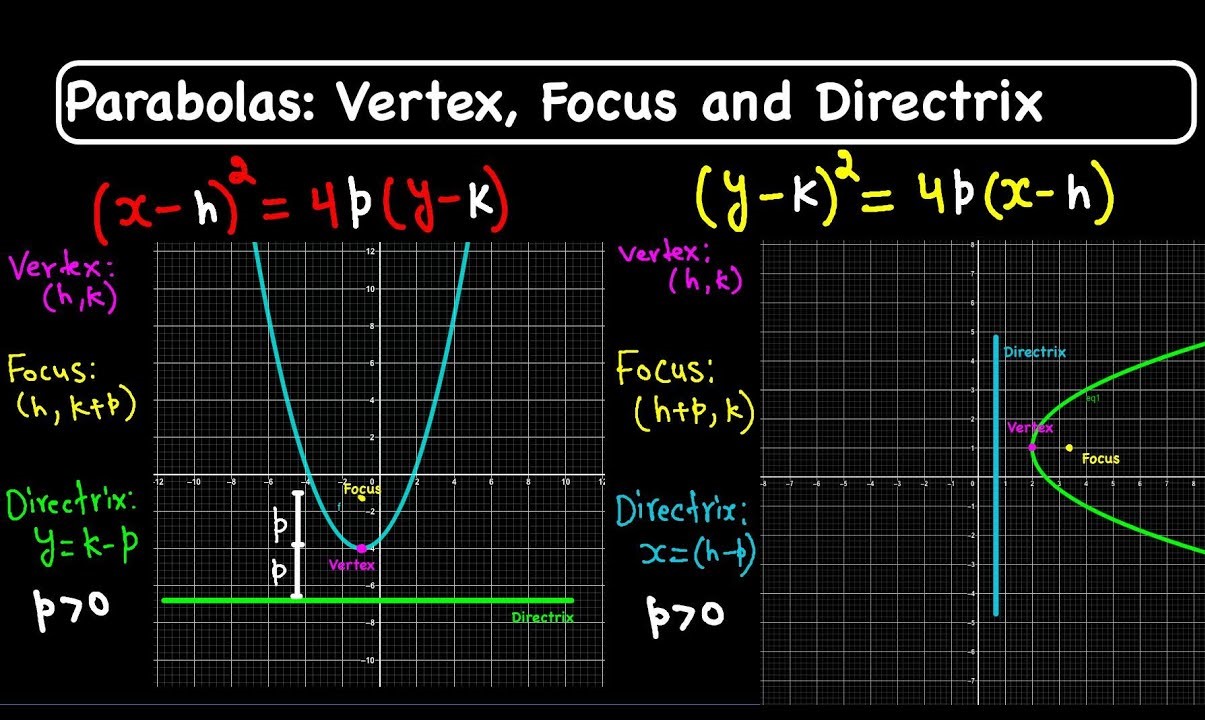
At the heart of every parabola lies a pivotal point known as the vertex. This singular point serves as the apex of the parabolic curve, embodying crucial geometric and algebraic significance. In essence, the vertex represents the point of transition for the parabola, marking the shift from its upward or downward trajectory. Understanding the vertex is essential for unraveling the behavior, orientation, and key properties of a parabola.

Geometrically, the vertex of a parabola is the point where the curve changes direction, transitioning from its ascent to descent or vice versa. This pivotal point is situated equidistant from the focus and the directrix, embodying the symmetrical essence of the parabolic curve. In essence, the vertex encapsulates the essence of equilibrium within the parabola, serving as the locus of balance and transition for the graceful curve.

Algebraically, the vertex of a parabola is represented as the point (h, k), where 'h' denotes the x-coordinate and 'k' signifies the y-coordinate. The standard form of a parabolic equation, y = ax^2 + bx + c, allows for the direct extraction of the vertex coordinates through the formula (-b/2a, f(-b/2a)), where 'f(x)' represents the parabolic function. This algebraic representation enables mathematicians and scientists to pinpoint the precise location of the vertex, facilitating the analysis and manipulation of parabolic curves with precision and insight.

Furthermore, the vertex serves as the focal point for understanding the orientation of a parabola. If the parabola opens upward, the vertex represents the lowest point on the curve, known as the minimum point. Conversely, if the parabola opens downward, the vertex serves as the highest point, denoted as the maximum point. This nuanced understanding of the vertex's role in determining the extremum of the parabola underscores its pivotal significance in analyzing the behavior and characteristics of these captivating curves.

Moreover, the vertex embodies an intrinsic connection to the axis of symmetry of a parabola, serving as the point of intersection for this pivotal line. The axis of symmetry, a vertical line that passes through the vertex, divides the parabola into two symmetrical halves, underscoring the inherent balance and harmony within the curve. This geometric relationship between the vertex and the axis of symmetry not only facilitates the visualization of parabolic symmetry but also enables mathematicians to discern patterns and properties inherent in these elegant curves.

In essence, the vertex of a parabola stands as a beacon of geometric elegance and algebraic precision, embodying the symmetrical beauty and analytical depth of these captivating curves. By mastering the concept of the vertex, individuals gain a profound understanding of the pivotal point that defines the essence of a parabola, empowering them to unravel its mysteries, analyze its behavior, and appreciate the profound elegance inherent in this fundamental geometric construct.

The Focus of a Parabola

The focus of a parabola holds a pivotal role in defining the geometric and optical properties of this captivating curve. Situated on the axis of symmetry, the focus represents a singular point that exerts a profound influence on the trajectory and reflective behavior of the parabola. Understanding the significance of the focus is essential for unraveling the enigmatic allure of parabolic curves and appreciating their omnipresence in diverse fields, from astronomy and physics to architecture and engineering.

Geometrically, the focus is the fixed point from which all the points on the parabola are equidistant to the directrix. This fundamental property underscores the symmetrical nature of the parabolic curve, highlighting the intrinsic balance and elegance embedded within its graceful arc. The precise location of the focus is determined by the distance from the vertex to the focus, denoted as the focal length, and serves as a defining characteristic that shapes the trajectory and reflective properties of the parabola.

Algebraically, the coordinates of the focus are represented as (h, k + 1/4a), where 'h' signifies the x-coordinate of the vertex, 'k' denotes the y-coordinate of the vertex, and 'a' represents the coefficient of the quadratic term in the parabolic equation. This algebraic representation enables mathematicians and scientists to pinpoint the exact position of the focus, facilitating the analysis and manipulation of parabolic curves with precision and insight.

Furthermore, the focus plays a crucial role in the reflective properties of parabolas, particularly in the realm of optics. When light or sound waves emanate from the focus of a parabolic reflector, they converge to form parallel rays or waves, harnessing the focusing power inherent in the parabolic shape. This phenomenon finds practical applications in diverse technologies, including satellite dishes, telescopes, and reflector antennas, where the reflective properties of parabolic curves enable the precise collection and transmission of electromagnetic signals.

In essence, the focus of a parabola embodies the essence of symmetry, precision, and optical elegance, serving as a focal point for understanding the geometric, algebraic, and practical significance of these captivating curves. By mastering the concept of the focus, individuals gain a profound appreciation for the pivotal role it plays in shaping the behavior, reflective properties, and practical applications of parabolas, empowering them to wield the mathematical prowess of these elegant curves with finesse and insight.

The Directrix of a Parabola

The directrix of a parabola is a fundamental element that defines the geometric and reflective properties of this captivating curve. Situated parallel to the axis of symmetry, the directrix serves as a fixed line that exerts a profound influence on the trajectory and optical behavior of the parabola. Understanding the significance of the directrix is essential for unraveling the enigmatic allure of parabolic curves and appreciating their omnipresence in diverse fields, from mathematics and physics to engineering and architecture.

Geometrically, the directrix is a horizontal line located at a specific distance from the vertex of the parabola. This fixed distance is determined by the focal length, which represents the distance from the vertex to the focus of the parabola. The directrix is positioned symmetrically opposite to the focus, underscoring the inherent balance and elegance within the parabolic curve. This geometric relationship between the directrix and the focus shapes the reflective properties of the parabola, influencing the behavior of light, sound, or other waves that interact with the curve.

Algebraically, the equation of the directrix is represented as y = k – 1/4a, where 'k' signifies the y-coordinate of the vertex, and 'a' represents the coefficient of the quadratic term in the parabolic equation. This algebraic representation enables mathematicians and scientists to precisely define the position and orientation of the directrix, facilitating the analysis and manipulation of parabolic curves with precision and insight.

Furthermore, the directrix plays a crucial role in understanding the reflective properties of parabolas, particularly in the realm of optics. When light or sound waves strike the parabolic curve, they reflect off its surface in such a way that the angle of incidence is equal to the angle of reflection, in accordance with the laws of physics. This phenomenon finds practical applications in diverse technologies, including satellite dishes, parabolic microphones, and reflective telescopes, where the reflective properties of parabolic curves enable the precise collection and transmission of electromagnetic signals.

In essence, the directrix of a parabola embodies the essence of symmetry, precision, and optical elegance, serving as a pivotal line for understanding the geometric, algebraic, and practical significance of these captivating curves. By mastering the concept of the directrix, individuals gain a profound appreciation for the crucial role it plays in shaping the behavior, reflective properties, and practical applications of parabolas, empowering them to wield the mathematical prowess of these elegant curves with finesse and insight.

Mastering the Art of Parabolas

Mastering the art of parabolas transcends mere comprehension; it entails embracing their inherent elegance, harnessing their mathematical prowess, and unleashing their practical applications. To truly master the art of parabolas is to embark on a transformative journey that empowers individuals to perceive the world through the lens of these captivating curves, unravel complex problems with precision, and appreciate the profound beauty embedded within their graceful arcs.

At the heart of mastering parabolas lies a deep understanding of their fundamental elements—the vertex, focus, and directrix. These defining components serve as the pillars upon which the edifice of parabolic mastery is built. By delving into the intricate relationships between these elements and discerning their geometric, algebraic, and practical significance, individuals gain a holistic comprehension of parabolas, enabling them to navigate their complexities with confidence and insight.

Moreover, mastering the art of parabolas involves honing the ability to manipulate and analyze parabolic equations with finesse and precision. By leveraging the canonical form of parabolic equations, individuals can discern patterns, identify key properties, and extract valuable insights into the behavior and characteristics of these captivating curves. This analytical prowess not only facilitates the solution of complex mathematical problems but also empowers individuals to apply the principles of parabolas in diverse fields, from physics and engineering to architecture and astronomy.

Furthermore, mastering parabolas extends beyond theoretical comprehension to practical applications. By recognizing the ubiquitous presence of parabolic shapes in the natural world and human-made structures, individuals can harness the power of parabolas to design innovative solutions, optimize technological devices, and unravel scientific phenomena. Whether it's designing a parabolic reflector for enhanced signal transmission or modeling the trajectory of a projectile, the practical mastery of parabolas unlocks a world of creative possibilities and technological advancements.

In essence, mastering the art of parabolas is a transformative endeavor that transcends the boundaries of traditional mathematical comprehension. It empowers individuals to perceive the world through the graceful arcs of parabolic curves, unravel the mysteries of nature and technology, and appreciate the profound elegance inherent in these fundamental geometric constructs. By embracing the art of parabolas, individuals embark on a journey of intellectual enrichment, creative exploration, and practical innovation, wielding the mathematical prowess of these captivating curves with finesse and insight.

Conclusion

In conclusion, the exploration of parabolas has unveiled a world of geometric elegance, algebraic precision, and practical significance. From the graceful arcs of projectile trajectories to the reflective properties of satellite dishes, parabolas permeate diverse fields, underscoring their universal relevance and captivating allure.

Throughout this journey, we have delved into the fundamental elements of parabolas—the vertex, focus, and directrix—unraveling their geometric, algebraic, and practical significance. The vertex, as the pivotal point of transition, embodies the essence of equilibrium within the parabola, serving as a beacon of geometric elegance and analytical depth. The focus, situated on the axis of symmetry, exerts a profound influence on the trajectory and reflective properties of the parabola, harnessing the power of symmetry and precision. The directrix, parallel to the axis of symmetry, shapes the reflective properties of the parabola, offering insights into its optical behavior and practical applications.

Mastering the art of parabolas transcends theoretical comprehension, empowering individuals to perceive the world through the lens of these captivating curves, unravel complex problems with precision, and appreciate the profound beauty embedded within their graceful arcs. By honing the ability to manipulate and analyze parabolic equations, individuals gain a holistic comprehension of parabolas, enabling them to navigate their complexities with confidence and insight. Furthermore, the practical mastery of parabolas unlocks a world of creative possibilities and technological advancements, fostering innovation and discovery across diverse fields.

In essence, the exploration of parabolas has not only enriched our understanding of fundamental mathematical concepts but also illuminated the pervasive influence of these captivating curves in the natural world and human endeavors. By embracing the art of parabolas, individuals embark on a transformative journey of intellectual enrichment, creative exploration, and practical innovation, wielding the mathematical prowess of these elegant curves with finesse and insight.

As we conclude this exploration, let us carry forth the profound appreciation for the elegance and utility of parabolas, recognizing their omnipresence in the fabric of our physical reality and the boundless opportunities they offer for creative expression, scientific discovery, and technological advancement. The art of parabolas beckons, inviting us to unravel its mysteries, harness its mathematical prowess, and embark on a journey of intellectual enrichment and practical innovation.