The Mind-Blowing Truth About Sin(-x) That Will Leave You Speechless!

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

When it comes to mathematics, certain functions have the power to captivate our imagination and challenge our understanding of the world around us. One such function that continues to baffle and intrigue mathematicians and students alike is the sin(-x) function. This seemingly enigmatic function holds within it a wealth of mathematical beauty and complexity that is waiting to be unraveled.

The sin(-x) function is a fundamental trigonometric function that represents the ratio of the length of the side opposite an acute angle in a right-angled triangle to the length of the hypotenuse. However, when the angle is negative, the sin(-x) function takes on a whole new dimension, leading to a fascinating journey into the realm of mathematical intricacies.

In this exploration, we will delve into the mind-blowing truth about sin(-x) that will leave you speechless. We will unravel the mysteries behind the graph of sin(-x), uncover the intriguing properties that define this function, and shed light on its wide-ranging applications in the real world. By the end of this journey, you will gain a newfound appreciation for the sin(-x) function and its profound impact on the world of mathematics and beyond. So, fasten your seatbelts and get ready to embark on an exhilarating mathematical adventure!

What is sin(-x)?

The sin(-x) function is a critical component of trigonometry, a branch of mathematics that deals with the relationships between the angles and sides of triangles. At its core, sin(-x) represents the sine of a negative angle, where the negative sign is applied to the angle itself. This concept may initially seem perplexing, as angles are typically measured in a counterclockwise direction from the positive x-axis, leading to questions about the interpretation of negative angles in trigonometric functions.

In the context of sin(-x), the negative angle can be visualized as a clockwise rotation from the positive x-axis. This unique interpretation of negative angles introduces a fascinating twist to the traditional understanding of trigonometric functions. As a result, the sin(-x) function yields a distinct set of values that reflect the sine of negative angles, offering a deeper insight into the symmetries and periodicity inherent in trigonometric functions.

When evaluating sin(-x), it is essential to recognize that the negative sign impacts the sign of the resulting sine value. Specifically, the sign of sin(-x) alternates based on the quadrant in which the angle -x resides. This phenomenon is intricately linked to the unit circle, where the geometric representation of angles and their trigonometric functions unveils the intricate interplay between positive and negative angles.

By understanding the essence of sin(-x) within the broader framework of trigonometry, we gain a profound appreciation for the interconnectedness of mathematical concepts and the elegant complexities that underpin the sin(-x) function. This deeper understanding not only enriches our mathematical knowledge but also opens the door to a world of applications where sin(-x) plays a pivotal role in modeling natural phenomena, engineering designs, and scientific inquiries.

In essence, the sin(-x) function transcends the conventional boundaries of trigonometry, inviting us to explore the profound implications of negative angles and their impact on the sine values. This exploration not only illuminates the intricacies of trigonometric functions but also serves as a testament to the boundless beauty and depth of mathematical concepts.

In summary, sin(-x) represents the sine of a negative angle, offering a unique perspective on trigonometric functions and their interplay with negative angles. This fundamental understanding forms the cornerstone of further explorations into the graph, properties, and applications of sin(-x), unveiling a world of mathematical wonder waiting to be discovered.

Graph of sin(-x)

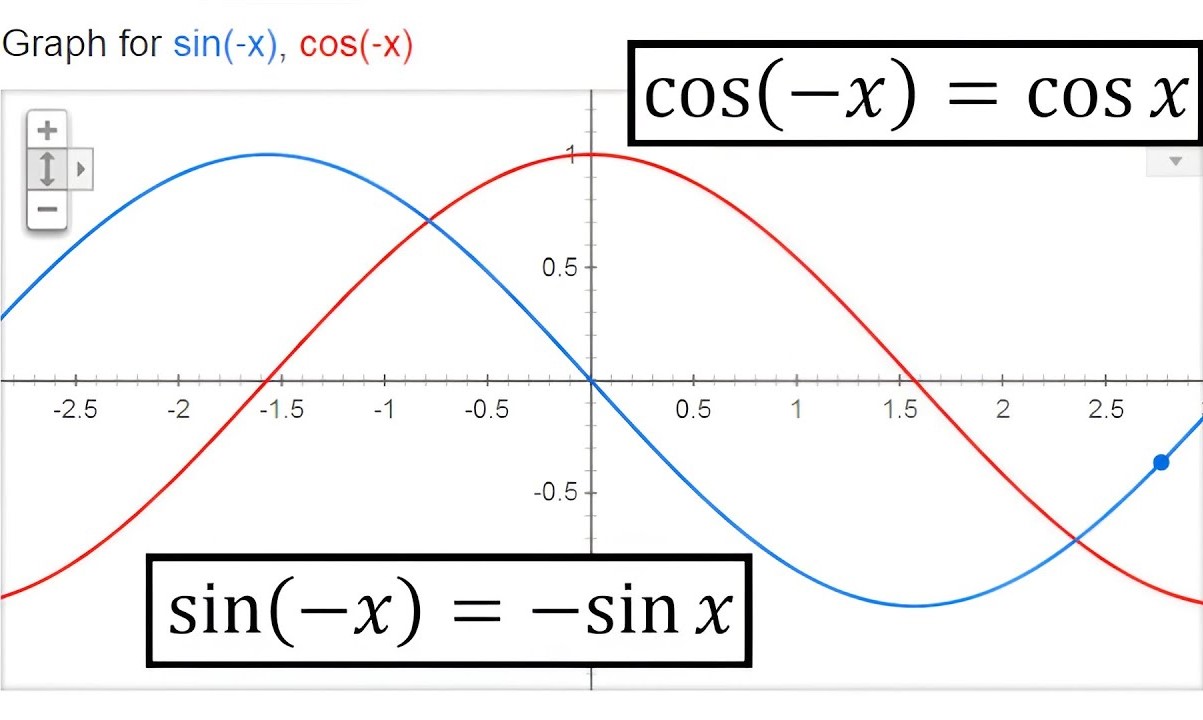
The graph of the sin(-x) function unveils a mesmerizing symmetrical pattern that reflects the interplay between negative angles and their corresponding sine values. When visualized on the Cartesian coordinate system, the graph of sin(-x) showcases a remarkable mirror image of the graph of sin(x) across the y-axis. This striking symmetry arises from the fundamental properties of the sine function, where the application of the negative sign to the angle -x leads to a reversal of direction along the x-axis, resulting in a visually captivating representation.

At the heart of the sin(-x) graph lies the profound relationship between negative angles and their sine values. As the angle -x traverses the quadrants of the unit circle, the corresponding sine values undergo a systematic transformation, giving rise to a wave-like pattern that oscillates between positive and negative values. This oscillatory behavior is elegantly captured in the graph of sin(-x), where the sinusoidal curve gracefully undulates, embodying the intrinsic periodicity of the sine function.

The graph of sin(-x) not only embodies symmetry and periodicity but also serves as a testament to the profound interconnectedness of trigonometric functions. By juxtaposing the graphs of sin(x) and sin(-x), a visually stunning juxtaposition emerges, highlighting the complementary nature of positive and negative angles within the realm of trigonometry. This juxtaposition offers a captivating visual insight into the duality of angles and their corresponding sine values, shedding light on the intricate balance between positive and negative rotations in the context of trigonometric functions.

Furthermore, the graph of sin(-x) provides a compelling visual representation of the unique characteristics of negative angles and their impact on the sine values. As the angle -x extends beyond the initial quadrant, the sine values undergo a transformative journey, reflecting the nuanced interplay between negative angles and the resulting sine function. This transformative journey is elegantly captured in the graph of sin(-x), offering a visually immersive experience that encapsulates the essence of negative angles within the broader tapestry of trigonometry.

In essence, the graph of sin(-x) serves as a captivating visual testament to the intricate symmetries, periodicities, and interdependencies that define the sin(-x) function. By immersing ourselves in the visual allure of this graph, we gain a deeper appreciation for the profound relationship between negative angles and their corresponding sine values, unveiling a world of mathematical beauty that transcends traditional boundaries and invites us to explore the boundless depths of trigonometry.

Properties of sin(-x)

The sin(-x) function exhibits a set of distinctive properties that distinguish it from its positive counterpart, sin(x), and contribute to its enigmatic allure. Understanding these properties is crucial for unraveling the intricate nature of the sin(-x) function and its profound implications in various mathematical contexts.

1. Symmetry: One of the defining properties of sin(-x) is its symmetry about the origin. This symmetry arises from the application of the negative sign to the angle -x, leading to a reversal of direction along the x-axis. As a result, the graph of sin(-x) is a mirror image of the graph of sin(x) across the y-axis, showcasing an exquisite symmetry that underscores the interplay between positive and negative angles within the realm of trigonometry.

2. Odd Function: The sin(-x) function possesses the characteristic of being an odd function. This means that it exhibits symmetry with respect to the origin, where f(-x) = -f(x) for all x in the domain of the function. The odd nature of sin(-x) underscores its unique behavior, where the application of the negative sign to the angle -x yields a sine value that is the negative of the corresponding sine value for the positive angle x. This fundamental property encapsulates the intrinsic symmetry and balance inherent in the sin(-x) function, offering a profound insight into its mathematical elegance.

3. Periodicity: Similar to sin(x), the sin(-x) function is periodic, with a period of 2π. This periodicity arises from the fundamental nature of the sine function, where the oscillatory behavior repeats itself every 2π units along the x-axis. However, in the case of sin(-x), the negative angle -x introduces a unique phase shift that imparts a distinct character to the periodic behavior of the function. This interplay between periodicity and negative angles yields a captivating insight into the intricate dynamics of the sin(-x) function, enriching our understanding of its fundamental properties.

4. Range: The range of the sin(-x) function is identical to that of sin(x), spanning the interval [-1, 1]. This range encapsulates the amplitude of the sine values for negative angles, showcasing the oscillatory nature of the sin(-x) function within the constrained range of [-1, 1]. By delineating the range of sin(-x), we gain a comprehensive understanding of the amplitude and variability of the sine values for negative angles, providing a holistic perspective on the behavior of the function across different quadrants.

In summary, the properties of sin(-x) encompass its symmetry, odd nature, periodicity, and range, offering a multifaceted insight into the captivating intricacies of this fundamental trigonometric function. By delving into these properties, we unravel the profound symmetries, periodicities, and interdependencies that define sin(-x, inviting us to explore the boundless depths of trigonometry.

Applications of sin(-x)

The sin(-x) function, with its unique properties and symmetrical nature, finds diverse applications across various fields, ranging from physics and engineering to signal processing and beyond. Its role in modeling periodic phenomena and capturing the dynamics of oscillatory systems makes it an indispensable tool in understanding natural and engineered systems.

In the realm of physics, the sin(-x) function plays a crucial role in describing wave propagation and harmonic motion. When analyzing the behavior of waves or oscillations in systems such as pendulums, springs, and vibrating structures, the sin(-x) function emerges as a fundamental building block for characterizing the displacement, velocity, and acceleration of these dynamic systems. By modeling the periodic nature of these phenomena, sin(-x) provides invaluable insights into the underlying dynamics of oscillatory systems, enabling physicists and engineers to predict and analyze the behavior of wave-like processes with precision.

Furthermore, in the field of electrical engineering and signal processing, the sin(-x) function is instrumental in representing alternating current (AC) circuits and signal waveforms. The application of sin(-x) in AC circuit analysis allows engineers to analyze the voltage and current variations in time-varying circuits, facilitating the design and optimization of electrical systems. Moreover, in signal processing, the sin(-x) function serves as a cornerstone for modeling periodic signals, enabling the analysis and synthesis of complex waveforms in communication systems, audio processing, and digital signal processing applications.

In the context of mathematical modeling, the sin(-x) function finds widespread use in capturing the behavior of oscillatory phenomena, including harmonic motion, periodic fluctuations, and cyclic processes. Its ability to represent the oscillatory nature of physical and natural phenomena makes it an indispensable tool for scientists and researchers seeking to understand and predict the dynamics of diverse systems, ranging from mechanical vibrations and acoustic waves to biological rhythms and ecological cycles.

Moreover, the symmetrical properties of sin(-x) make it a valuable asset in mathematical transformations and symmetry operations, providing a powerful framework for analyzing and manipulating mathematical structures in diverse domains, including geometry, algebra, and calculus.

In essence, the applications of sin(-x) extend far beyond the realm of pure mathematics, permeating into the fabric of scientific inquiry, engineering design, and technological innovation. Its capacity to capture the periodic and oscillatory nature of diverse phenomena underscores its indispensable role in understanding the fundamental dynamics of the natural and engineered world, making it an enduring cornerstone of mathematical and scientific exploration.

Conclusion

In conclusion, the sin(-x) function encapsulates a world of mathematical wonder, symmetry, and profound interconnectedness that transcends traditional boundaries and invites us to explore the boundless depths of trigonometry. From unraveling the mesmerizing graph of sin(-x) to delving into its distinctive properties and diverse applications, our journey has illuminated the captivating intricacies and far-reaching impact of this fundamental trigonometric function.

The exploration of sin(-x) has revealed its symmetrical nature, where the application of the negative sign to the angle -x yields a mirror image of the graph of sin(x) across the y-axis, showcasing an exquisite symmetry that underscores the interplay between positive and negative angles within the realm of trigonometry. This symmetrical property not only unveils the profound balance and harmony inherent in the sin(-x) function but also provides a visually immersive experience that encapsulates the essence of negative angles within the broader tapestry of trigonometry.

Furthermore, the properties of sin(-x), including its odd nature, periodicity, and range, have enriched our understanding of the intricate dynamics and interconnectedness that define this fundamental trigonometric function. The odd nature of sin(-x) underscores its unique behavior, offering a profound insight into its mathematical elegance, while its periodicity and constrained range provide a holistic perspective on the behavior of the function across different quadrants, enriching our understanding of its fundamental properties.

Moreover, the applications of sin(-x) across diverse fields, from physics and engineering to signal processing and mathematical modeling, underscore its indispensable role in understanding natural and engineered systems. Its capacity to capture the periodic and oscillatory nature of diverse phenomena permeates into the fabric of scientific inquiry, engineering design, and technological innovation, making it an enduring cornerstone of mathematical and scientific exploration.

In essence, the mind-blowing truth about sin(-x) has left us with a profound appreciation for the interconnectedness of mathematical concepts and the boundless beauty and depth of trigonometric functions. As we conclude this exhilarating mathematical adventure, we are reminded that the sin(-x) function, with its symmetrical allure, distinctive properties, and wide-ranging applications, continues to inspire and challenge our understanding of the world around us, inviting us to embrace the captivating complexities that define the sin(-x) function and its enduring impact on the realm of mathematics and beyond.