The Ultimate Guide To Calculating Triangle Bases: Master The Art Of Geometry!

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Welcome to the fascinating world of geometry, where shapes and figures come to life through the magic of mathematics. In this comprehensive guide, we will embark on a journey to unravel the mysteries of calculating triangle bases. As we delve into the intricate realm of triangles, we will uncover the fundamental principles and techniques that govern the determination of their bases.

Triangles are among the most fundamental shapes in geometry, characterized by their three sides and three angles. The base of a triangle plays a pivotal role in defining its properties and is crucial for various calculations and real-world applications. By mastering the art of calculating triangle bases, you will gain a deeper understanding of geometric principles and unleash the potential to solve a myriad of problems with precision and confidence.

Throughout this guide, we will explore the diverse types of triangles, from the classic right-angled triangle to the elegant equilateral and isosceles triangles, and the versatile scalene triangle. Each type presents unique challenges and opportunities when it comes to determining their bases, and we will equip you with the knowledge and skills to conquer them all.

Additionally, we will unravel the mysteries of the Pythagorean Theorem, a cornerstone of geometry that holds the key to unlocking the secrets of right-angled triangles. By understanding this powerful theorem, you will uncover a wealth of insights into the relationships between the sides of a right-angled triangle and pave the way for seamless base calculations.

As we progress, we will not only focus on the theoretical aspects of calculating triangle bases but also delve into practical applications that showcase the real-world significance of these mathematical concepts. From architecture and engineering to art and design, the ability to calculate triangle bases is a valuable skill that transcends the boundaries of the classroom and resonates across diverse fields.

So, prepare to embark on an enlightening journey through the captivating realm of geometry as we unravel the enigma of triangle bases. By the time you reach the end of this guide, you will emerge as a master of geometric calculations, armed with the knowledge and confidence to tackle any triangle base with finesse and precision. Let's dive in and unlock the secrets of triangle bases together!

Understanding Triangle Bases

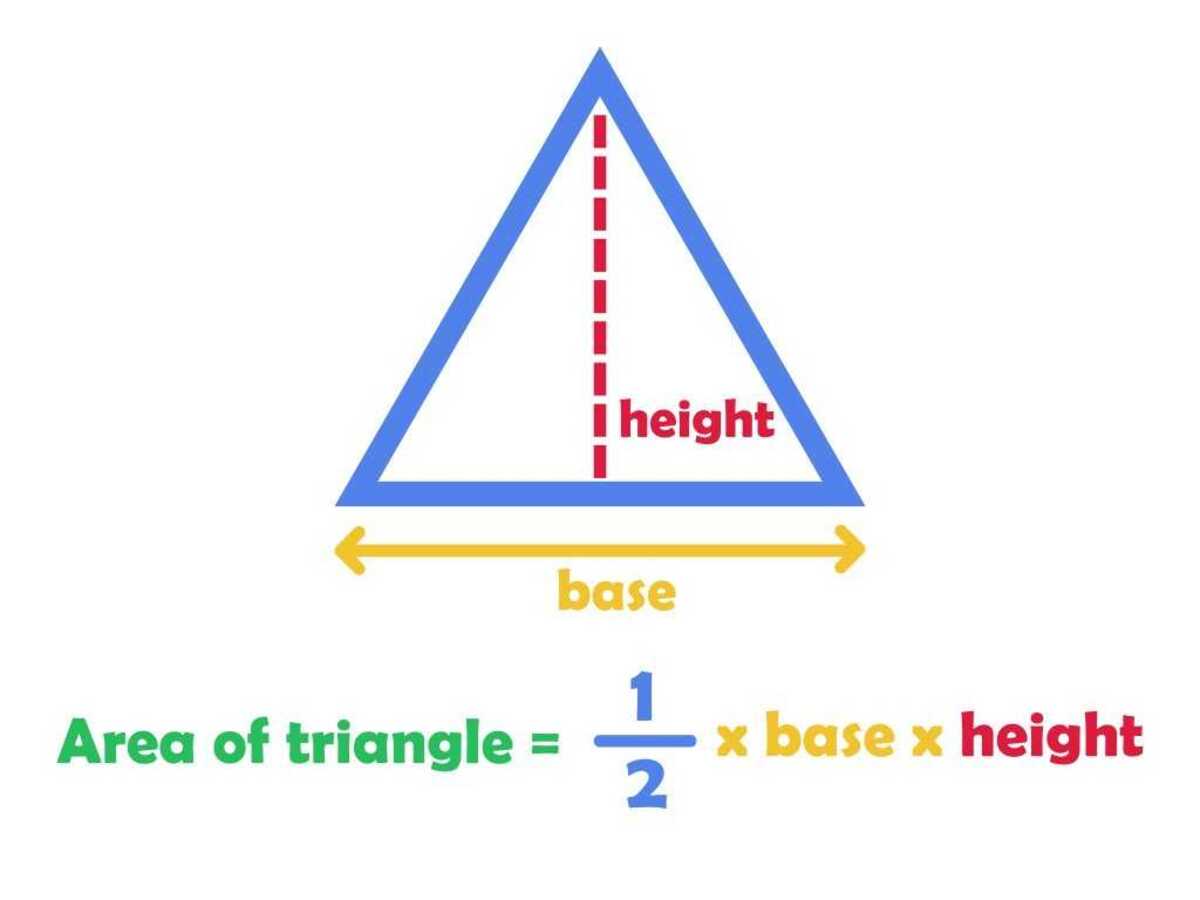
The concept of a triangle base forms the cornerstone of understanding the fundamental properties and calculations associated with triangles. In a triangle, the base refers to the side on which the triangle rests, providing a stable foundation for its structure. It is important to note that the base of a triangle is not necessarily limited to the bottom side; rather, it depends on the orientation of the triangle and the context in which it is being analyzed.

In a right-angled triangle, the base is typically considered as the side opposite the right angle, while in an isosceles triangle, it is the non-equal side. For equilateral triangles, all three sides are effectively bases, given their identical lengths. The base of a scalene triangle, on the other hand, is simply one of the three unequal sides. Understanding these distinctions is crucial for accurately identifying and calculating triangle bases in various scenarios.

The length of the base directly influences the calculation of the triangle's area and perimeter, making it a critical parameter in geometric computations. Furthermore, the base serves as a reference point for determining the height of the triangle, which is essential for area calculations. The relationship between the base and height of a triangle is a fundamental aspect of geometric principles, and mastering this connection is key to unlocking the mysteries of triangle bases.

Beyond its geometric significance, the concept of a triangle base extends into practical applications across diverse fields. From architectural blueprints and structural engineering to artistic compositions and design layouts, the understanding of triangle bases underpins the creation and analysis of countless real-world structures and visual elements. By comprehending the intricacies of triangle bases, individuals gain the ability to deconstruct and analyze complex shapes with precision and insight.

In essence, understanding triangle bases transcends the realm of abstract mathematics and emerges as a foundational skill with tangible implications. It empowers individuals to perceive and manipulate the geometric world around them, fostering a deeper appreciation for the elegance and utility of mathematical principles. As we continue our exploration of triangle bases, we will unravel the techniques and methodologies for calculating bases across various types of triangles, equipping you with the knowledge and confidence to navigate the intricate landscape of geometric calculations.

The Pythagorean Theorem

The Pythagorean Theorem stands as a timeless testament to the profound interplay between geometry, algebra, and number theory. At its core, this fundamental principle unveils a captivating relationship between the sides of a right-angled triangle, offering a gateway to unraveling the mysteries of geometric configurations.

Expressed as a simple yet profound equation, a^2 + b^2 = c^2, the Pythagorean Theorem embodies the essence of mathematical elegance, where the squares of the two shorter sides of a right-angled triangle sum up to the square of the hypotenuse. This elegant relationship forms the cornerstone of countless geometric calculations, paving the way for a deeper understanding of spatial relationships and structural dynamics.

The implications of the Pythagorean Theorem extend far beyond its initial formulation, permeating diverse fields and applications. From architecture and engineering to navigation and surveying, the theorem serves as a guiding light, illuminating the pathways to precise measurements and structural stability. Its influence transcends the boundaries of mathematics, resonating across disciplines and shaping the very fabric of our physical world.

Moreover, the Pythagorean Theorem embodies a timeless elegance that transcends the confines of theoretical mathematics, captivating the imagination and intellect of scholars and enthusiasts for centuries. Its pervasive influence in art, music, and philosophy underscores the profound impact of mathematical principles on human creativity and expression.

In essence, the Pythagorean Theorem stands as a testament to the enduring power of mathematical concepts, weaving a tapestry of connections that bridge the abstract realm of numbers with the tangible world of shapes and structures. As we navigate the intricate landscape of geometric calculations, the Pythagorean Theorem serves as a guiding star, illuminating the path to a deeper understanding of spatial relationships and geometric configurations.

Calculating the Base of a Right-Angled Triangle

When it comes to calculating the base of a right-angled triangle, the Pythagorean Theorem emerges as a beacon of insight, offering a direct pathway to unraveling the length of this crucial side. In a right-angled triangle, the base represents the side that forms the foundation of the triangle and is positioned opposite the right angle.

To calculate the base of a right-angled triangle, one must first identify the other two sides: the perpendicular side (height) and the hypotenuse. The perpendicular side, often denoted as the 'height' of the triangle, extends vertically from the right angle to the opposite vertex, forming a 90-degree angle with the base. The hypotenuse, on the other hand, is the longest side of the triangle and is positioned opposite the right angle.

By leveraging the Pythagorean Theorem, which states that the square of the hypotenuse is equal to the sum of the squares of the other two sides, we can derive a straightforward method for calculating the base of a right-angled triangle. The theorem is expressed as follows: a^2 + b^2 = c^2, where 'a' and 'b' denote the lengths of the perpendicular and base, respectively, and 'c' represents the length of the hypotenuse.

To solve for the base, one can rearrange the equation to isolate the base length, yielding the formula: b = √(c^2 – a^2). Here, 'c' represents the length of the hypotenuse, and 'a' denotes the height of the triangle. By substituting these values into the formula, one can effortlessly determine the length of the base, thus completing the essential trio of side measurements for the right-angled triangle.

This elegant approach to calculating the base of a right-angled triangle showcases the seamless integration of geometric principles and algebraic techniques, underscoring the interconnected nature of mathematical concepts. By mastering this fundamental calculation, individuals gain a powerful tool for analyzing and manipulating right-angled triangles, unlocking a world of geometric possibilities and practical applications.

In essence, the process of calculating the base of a right-angled triangle exemplifies the harmonious fusion of mathematical theory and real-world problem-solving, empowering individuals to navigate the intricate landscape of geometry with confidence and precision.

Calculating the Base of an Equilateral Triangle

In the realm of geometric elegance, the equilateral triangle stands as a paragon of symmetry and balance, captivating the imagination with its uniform sides and harmonious angles. When it comes to calculating the base of an equilateral triangle, the inherent symmetry and equality of its sides present a captivating challenge that unveils the beauty of geometric relationships.

In an equilateral triangle, all three sides are equal in length, and each angle measures 60 degrees. This uniformity gives rise to a captivating interplay of geometric properties, where the base of the triangle is effectively shared among all three sides. Unlike other types of triangles where the base is distinctly defined, the equilateral triangle presents a unique scenario where every side can be considered as a base, depending on the context of the analysis.

To calculate the base of an equilateral triangle, one can leverage the intrinsic symmetry and equality of its sides. Given the uniformity of the triangle, any side can serve as the base, allowing for flexibility in approaching base calculations. This characteristic symmetry also extends to the height of the equilateral triangle, where the perpendicular line from any vertex to the opposite side bisects the base, forming two congruent right-angled triangles.

The relationship between the sides and angles of an equilateral triangle gives rise to a fascinating method for calculating the base. By dividing the equilateral triangle into two congruent right-angled triangles using the perpendicular line from a vertex to the midpoint of the opposite side, one can apply trigonometric principles to determine the base length. Specifically, the trigonometric function of sine, which relates the opposite side to the hypotenuse in a right-angled triangle, can be employed to calculate the base length.

Expressed as sin(60°) = opposite/hypotenuse, the trigonometric relationship offers a direct pathway to calculating the base length of the equilateral triangle. Given that sin(60°) equals the square root of 3 divided by 2, multiplying this value by the length of any side yields the base length. This elegant approach showcases the seamless integration of trigonometric principles with the inherent symmetry of the equilateral triangle, unveiling a captivating method for base calculations.

In essence, the process of calculating the base of an equilateral triangle illuminates the profound interplay of symmetry, trigonometry, and geometric elegance, underscoring the captivating beauty of mathematical relationships. By mastering this calculation, individuals gain a deeper appreciation for the harmonious principles that govern the equilateral triangle, unlocking a world of geometric insights and practical applications.

Calculating the Base of an Isosceles Triangle

When it comes to the enigmatic realm of triangles, the isosceles triangle emerges as a captivating archetype of symmetry and balance. Defined by its two equal sides and two congruent angles, the isosceles triangle presents a captivating challenge when it comes to calculating its base. The inherent symmetry and balance of this geometric wonder pave the way for a unique method of determining the base length, unveiling the seamless fusion of geometric principles and algebraic insights.

In an isosceles triangle, the base is defined as the unequal side that does not possess the symmetry of the equal sides and angles. This distinct characteristic sets the stage for a captivating exploration of geometric relationships, where the base serves as a foundational parameter for calculating the triangle's area, perimeter, and height. Understanding the interplay between the base and the equal sides is crucial for unraveling the mysteries of the isosceles triangle and leveraging its inherent symmetry to unlock geometric insights.

To calculate the base of an isosceles triangle, one can leverage the symmetry of the triangle to derive a direct method for determining its length. Given the equality of the two equal sides, the base divides the isosceles triangle into two congruent right-angled triangles, each sharing the same base length. This intriguing property forms the basis for a straightforward approach to calculating the base, where the Pythagorean Theorem emerges as a guiding light.

By applying the Pythagorean Theorem to one of the congruent right-angled triangles, one can derive a simple formula for calculating the base length. The theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. In the context of an isosceles triangle, the equal sides serve as the two shorter sides of the right-angled triangle, while the base represents the hypotenuse. By rearranging the theorem to solve for the base length, one can obtain a concise formula that encapsulates the elegance of the base calculation process.

Expressed as b = √(2a^2 – c^2), where 'b' denotes the base length, 'a' represents the length of the equal sides, and 'c' signifies the length of the base. This elegant formula encapsulates the essence of calculating the base of an isosceles triangle, showcasing the seamless integration of geometric properties and algebraic techniques. By mastering this fundamental calculation, individuals gain a powerful tool for analyzing and manipulating isosceles triangles, unlocking a world of geometric possibilities and practical applications.

In essence, the process of calculating the base of an isosceles triangle exemplifies the harmonious fusion of mathematical theory and real-world problem-solving, empowering individuals to navigate the intricate landscape of geometry with confidence and precision.

Calculating the Base of a Scalene Triangle

In the realm of geometric diversity, the scalene triangle stands as a captivating embodiment of asymmetry and uniqueness. Defined by its three unequal sides and angles, the scalene triangle presents an intriguing challenge when it comes to calculating its base. Unlike the equilateral or isosceles triangles, where the base may possess inherent symmetry or equality, the scalene triangle offers a distinctive scenario that requires a nuanced approach to determining the base length.

To calculate the base of a scalene triangle, one must first understand the inherent asymmetry and lack of congruence among its sides and angles. Unlike the other types of triangles where specific relationships or symmetries govern the base, the scalene triangle presents a scenario where each side can potentially serve as the base, depending on the context of the analysis. This characteristic diversity sets the stage for a captivating exploration of geometric relationships, where the base serves as a foundational parameter for calculating the triangle's area, perimeter, and height.

Given the absence of inherent symmetry or congruence among the sides, the process of calculating the base of a scalene triangle requires a meticulous approach that leverages the principles of trigonometry and geometric insights. By dissecting the scalene triangle into two right-angled triangles using a perpendicular line from a vertex to the opposite side, one can apply trigonometric principles to determine the base length.

The trigonometric function of sine, which relates the opposite side to the hypotenuse in a right-angled triangle, offers a compelling pathway to calculating the base length. By identifying the appropriate angle and side within the dissected right-angled triangles, one can apply the sine function to derive the base length. This elegant approach showcases the seamless integration of trigonometric principles with the inherent diversity of the scalene triangle, unveiling a captivating method for base calculations.

In essence, the process of calculating the base of a scalene triangle illuminates the profound interplay of asymmetry, trigonometry, and geometric diversity, underscoring the captivating beauty of mathematical relationships. By mastering this calculation, individuals gain a deeper appreciation for the nuanced principles that govern the scalene triangle, unlocking a world of geometric insights and practical applications.

Practical Applications of Calculating Triangle Bases

The practical applications of calculating triangle bases extend across a diverse array of fields, showcasing the real-world significance of these fundamental geometric calculations. From architecture and engineering to art and design, the ability to determine triangle bases plays a pivotal role in shaping and analyzing various structures, compositions, and visual elements.

In the realm of architecture and structural engineering, the calculation of triangle bases is essential for designing and constructing stable and resilient frameworks. Whether it involves the roof trusses of a building, the support beams of a bridge, or the framework of a dome, understanding the base of the underlying triangles is crucial for ensuring structural integrity. By accurately determining the bases of triangles within complex architectural designs, engineers and architects can optimize load distribution, minimize material usage, and enhance the overall stability of the structures.

Moreover, in the field of surveying and land measurement, the calculation of triangle bases is instrumental for mapping and delineating land parcels with precision. By leveraging the principles of trigonometry and geometry, surveyors can utilize the bases of triangles to calculate distances, establish boundaries, and create accurate topographic maps. This application of triangle base calculations contributes to urban planning, land development, and environmental conservation efforts, facilitating informed decision-making and sustainable land use practices.

In artistic and design contexts, the understanding of triangle bases serves as a cornerstone for creating visually compelling compositions and layouts. Whether in the realm of graphic design, photography, or visual arts, the ability to manipulate the bases of triangles influences the balance, symmetry, and visual impact of artistic creations. By leveraging the principles of geometry and proportion, artists and designers can harness the calculated bases of triangles to create harmonious and aesthetically pleasing arrangements, enhancing the overall impact of their work.

Furthermore, in the realm of manufacturing and fabrication, the calculation of triangle bases is integral for optimizing material usage and precision in production processes. Whether in the cutting of materials for industrial components or the fabrication of intricate patterns, the ability to determine triangle bases enables manufacturers to minimize waste, maximize efficiency, and ensure the dimensional accuracy of the final products.

In essence, the practical applications of calculating triangle bases permeate diverse fields and disciplines, underpinning the creation, analysis, and optimization of structures, designs, and visual compositions. By mastering the art of determining triangle bases, individuals gain a versatile and valuable skill set that transcends the boundaries of theoretical mathematics and resonates across the practical landscapes of science, engineering, art, and beyond.

Conclusion

In conclusion, the journey through the intricacies of calculating triangle bases has unveiled a captivating tapestry of geometric insights, practical applications, and timeless principles. From the foundational concepts of triangle bases to the diverse methods of calculation across different triangle types, this exploration has illuminated the profound interplay of symmetry, diversity, and elegance within the realm of geometry.

Mastering the art of calculating triangle bases transcends the confines of abstract mathematics and emerges as a foundational skill with tangible implications across various fields. Whether in architecture, engineering, art, or manufacturing, the ability to determine triangle bases empowers individuals to analyze, create, and optimize structures, designs, and visual compositions with precision and insight.

The Pythagorean Theorem has stood the test of time as a guiding light, illuminating the relationships between the sides of right-angled triangles and paving the way for seamless base calculations. This timeless principle embodies the enduring power of mathematical concepts, weaving a tapestry of connections that bridge the abstract realm of numbers with the tangible world of shapes and structures.

The symmetrical elegance of equilateral triangles, the balanced harmony of isosceles triangles, and the unique diversity of scalene triangles have each presented captivating challenges and opportunities in the realm of base calculations. Leveraging trigonometric principles, algebraic insights, and geometric properties, individuals can navigate the intricacies of each triangle type, unlocking a wealth of insights and practical applications.

Moreover, the practical applications of calculating triangle bases extend far beyond the confines of theoretical mathematics, permeating diverse fields and disciplines. From architectural stability and land surveying to artistic compositions and manufacturing precision, the ability to determine triangle bases serves as a cornerstone for innovation, efficiency, and creativity in real-world scenarios.

As we conclude this enlightening journey through the captivating realm of geometry, the mastery of calculating triangle bases emerges as a testament to the enduring relevance and beauty of mathematical principles. By embracing the elegance and utility of these calculations, individuals gain a deeper appreciation for the intricate interplay of shapes, numbers, and real-world applications, fostering a profound connection between theoretical concepts and practical significance.

In essence, the art of calculating triangle bases unveils a world of geometric possibilities, where symmetry, diversity, and practicality converge to shape the very fabric of our physical and intellectual landscapes. As we navigate the intricate terrain of geometric calculations, the mastery of triangle bases serves as a guiding star, illuminating the path to a deeper understanding of spatial relationships, structural dynamics, and the timeless beauty of mathematical principles.