The Ultimate Guide To Finding The Normal Vector And Direction Of A Plane!

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Understanding the concept of normal vectors and the direction of a plane is fundamental in various fields, including mathematics, physics, engineering, and computer graphics. In this comprehensive guide, we will delve into the intricacies of finding the normal vector and determining the direction of a plane. By the end of this exploration, you will gain a deep understanding of these concepts and their practical applications.

The normal vector of a plane is a crucial element that defines the orientation of the plane in three-dimensional space. It is perpendicular to the plane and provides essential information about the plane's orientation and inclination. Understanding how to find the normal vector of a plane is essential for solving geometric problems, analyzing spatial relationships, and performing vector operations.

Moreover, determining the direction of a plane is equally significant, as it allows us to discern how the plane extends infinitely in space. By comprehending the direction of a plane, we can accurately interpret its spatial orientation and its relationship to other geometric entities.

Throughout this guide, we will explore the underlying principles of normal vectors and plane direction, providing clear explanations and practical examples to facilitate your understanding. Whether you are a student grappling with vector mathematics or a professional seeking to apply these concepts in real-world scenarios, this guide will equip you with the knowledge and skills to navigate the complexities of normal vectors and plane direction with confidence.

Join us on this enlightening journey as we unravel the mysteries of normal vectors and plane direction, empowering you to approach mathematical and spatial challenges with clarity and proficiency. Let's embark on this exploration and unlock the secrets of the normal vector and the direction of a plane!

Understanding the Normal Vector

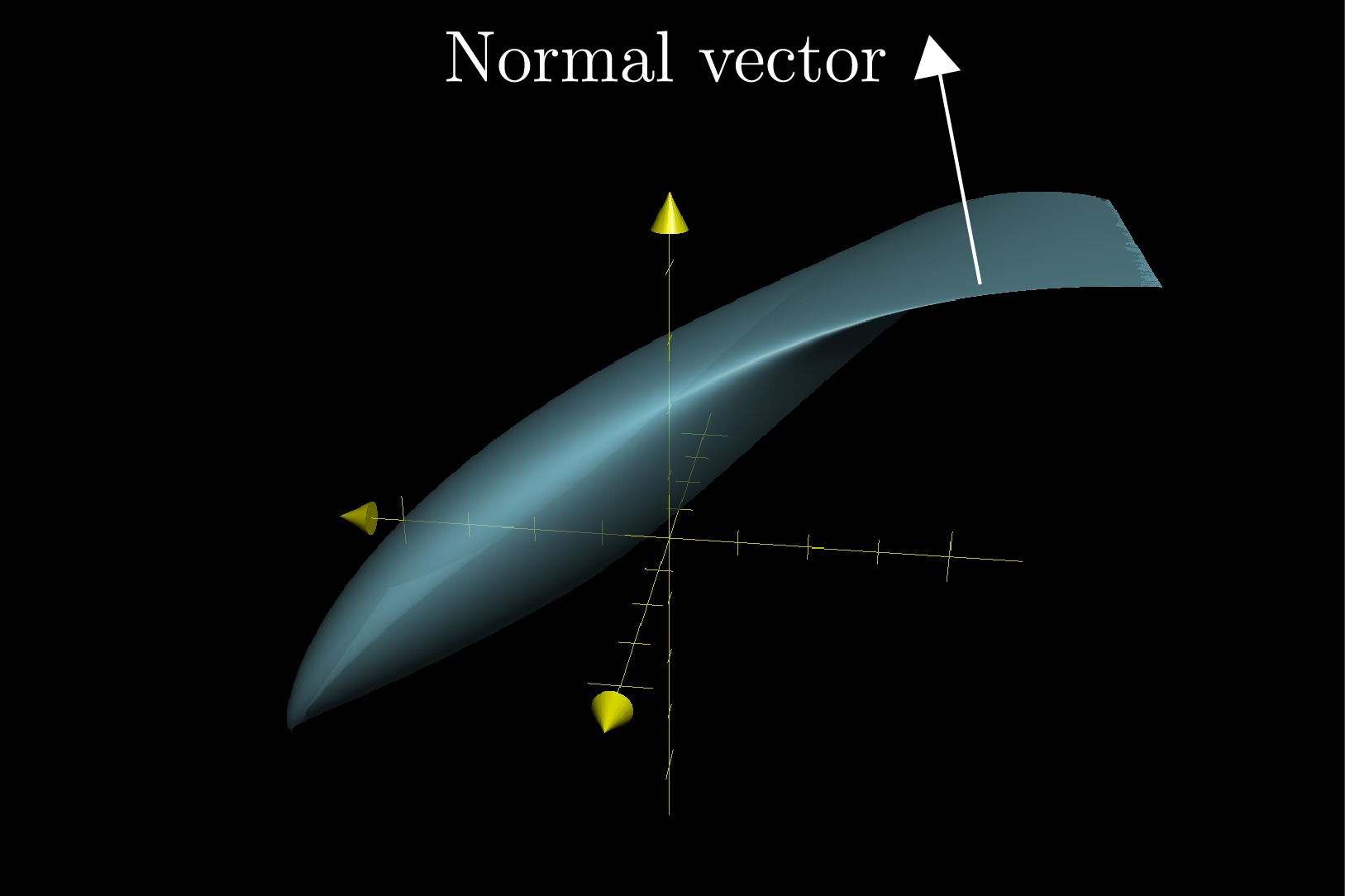
The normal vector of a plane plays a pivotal role in defining the orientation and spatial characteristics of the plane within a three-dimensional (3D) space. It is a vector that is perpendicular, or orthogonal, to the plane, meaning it extends directly away from the plane at a 90-degree angle. This fundamental property makes the normal vector an indispensable tool in geometric analysis, engineering, physics, and computer graphics.

In essence, the normal vector encapsulates the essential information about the orientation and inclination of the plane. It provides a clear indication of how the plane is positioned within 3D space, aiding in the visualization and manipulation of geometric entities.

When visualizing the normal vector, imagine it as an arrow that protrudes from the plane, pointing in a direction perpendicular to the plane's surface. This vector is crucial in determining the plane's orientation relative to other geometric elements, such as lines, curves, and other planes.

Understanding the normal vector involves grasping its geometric significance and its relationship to the plane it represents. By comprehending the normal vector, one gains insights into how the plane is oriented in space and how it interacts with other spatial entities.

Moreover, the normal vector serves as a key component in various mathematical operations, such as determining the angle between two planes, calculating the distance from a point to a plane, and solving systems of linear equations. Its utility extends beyond pure geometry, permeating into diverse fields where spatial relationships and vector operations are paramount.

In summary, the normal vector is a foundational concept that underpins the spatial orientation of a plane in 3D space. Its perpendicular nature to the plane's surface endows it with intrinsic geometric significance, making it an indispensable tool in mathematical, engineering, and scientific endeavors. By delving into the intricacies of the normal vector, one gains a deeper understanding of spatial relationships and geometric properties, paving the way for insightful interpretations and practical applications in various domains.

Finding the Normal Vector of a Plane

To find the normal vector of a plane, we can employ various approaches, with each method offering a unique perspective on the plane's orientation in 3D space. One of the most intuitive methods involves leveraging the coefficients of the plane's equation. In the context of a plane defined by the equation Ax + By + Cz = D, the coefficients A, B, and C directly correspond to the components of the normal vector. Thus, the normal vector N can be expressed as N = (A, B, C).

Another method for determining the normal vector involves considering the cross product of two non-parallel vectors lying in the plane. By selecting two distinct points on the plane and creating vectors from the origin to each point, we can calculate the cross product of these vectors to obtain the normal vector. This technique aligns with the fundamental properties of the cross product, yielding a vector that is perpendicular to both input vectors and, consequently, orthogonal to the plane.

Furthermore, if the plane is represented in parametric form as r(u, v) = p + u * a + v * b, where p is a point on the plane and a and b are vectors lying in the plane, the normal vector can be obtained by taking the cross product of vectors a and b. This method provides a geometrically intuitive approach to finding the normal vector, as it leverages the inherent properties of vectors in 3D space.

In addition to these methods, linear algebra offers a systematic approach to computing the normal vector using matrix operations. By representing the coefficients of the plane's equation in matrix form, we can perform operations to obtain the normal vector. This approach aligns with the principles of linear transformations and matrix operations, providing a rigorous and structured method for finding the normal vector.

In summary, the process of finding the normal vector of a plane encompasses various techniques rooted in geometry, linear algebra, and vector calculus. These methods offer diverse perspectives on the plane's orientation in 3D space, catering to different problem-solving contexts and mathematical frameworks. By mastering the art of finding the normal vector, one gains a powerful tool for analyzing spatial relationships, solving geometric problems, and understanding the fundamental properties of planes in three dimensions.

Determining the Direction of a Plane

Determining the direction of a plane is essential for understanding how the plane extends infinitely in three-dimensional space. It provides valuable insights into the spatial orientation of the plane and its relationship to other geometric entities. In essence, the direction of a plane elucidates the path along which the plane extends indefinitely, shedding light on its spatial characteristics and geometric significance.

One fundamental approach to determining the direction of a plane involves examining the coefficients of the plane's equation. In the standard form Ax + By + Cz = D, the coefficients A, B, and C not only define the normal vector but also encapsulate the directional information of the plane. By interpreting these coefficients as a vector, we can discern the direction in which the plane extends in 3D space. This directional vector provides a clear indication of how the plane propagates infinitely, offering crucial geometric insights into its spatial orientation.

Moreover, the direction of a plane can be visualized through the use of directional cosines, which represent the cosines of the angles between the plane and each of the coordinate axes. By calculating the directional cosines, we can articulate the spatial orientation of the plane and its alignment with the x, y, and z axes. This approach facilitates a comprehensive understanding of how the plane extends in space and how it aligns with the fundamental axes of the 3D coordinate system.

Furthermore, the direction of a plane can be inferred from its parametric representation. In the parametric form r(u, v) = p + ua + vb, where p is a point on the plane and a, b are vectors lying in the plane, the vectors a and b delineate the direction of the plane. By examining the relationship between these directional vectors and their influence on the plane's spatial extension, we can elucidate the directional characteristics of the plane with precision and clarity.

In summary, determining the direction of a plane involves interpreting the coefficients of its equation, calculating directional cosines, and analyzing the influence of directional vectors in its parametric representation. By engaging with these methodologies, one can unravel the spatial orientation and directional attributes of a plane, paving the way for insightful interpretations and practical applications in diverse mathematical, engineering, and scientific domains.

Conclusion

In conclusion, the exploration of normal vectors and the direction of planes has unveiled the profound significance of these concepts in the realm of mathematics, geometry, and spatial analysis. By delving into the intricacies of finding the normal vector and determining the direction of a plane, we have gained valuable insights into the spatial orientation, geometric properties, and practical applications of these fundamental elements.

The understanding of normal vectors as vectors perpendicular to planes has empowered us to comprehend the spatial orientation of planes in three-dimensional space. By visualizing normal vectors as arrows protruding from planes, pointing in a direction orthogonal to the plane's surface, we have grasped their pivotal role in defining the orientation and inclination of planes. Moreover, the diverse methods for finding the normal vector, including leveraging the coefficients of the plane's equation, utilizing the cross product of vectors, and employing parametric representations, have equipped us with versatile tools for analyzing spatial relationships and solving geometric problems.

Furthermore, the determination of the direction of a plane has provided us with crucial insights into how planes extend infinitely in 3D space. By interpreting the coefficients of the plane's equation as a directional vector and calculating directional cosines, we have elucidated the spatial orientation and alignment of planes with the fundamental axes of the coordinate system. Additionally, exploring the directional attributes of planes through their parametric representations has enriched our understanding of how planes propagate in space and interact with other geometric entities.

In essence, the knowledge and skills acquired in this comprehensive guide will serve as invaluable assets in tackling mathematical challenges, spatial analysis, and real-world applications across diverse domains. Whether in the realms of engineering, physics, computer graphics, or mathematical modeling, the ability to comprehend and manipulate normal vectors and plane directions is indispensable.

By mastering the art of finding the normal vector and determining the direction of a plane, we are poised to navigate the complexities of spatial relationships, geometric analysis, and vector operations with confidence and proficiency. This journey of exploration has not only deepened our understanding of these fundamental concepts but has also broadened our perspectives on spatial orientation and geometric properties, empowering us to approach mathematical and spatial challenges with clarity and insight.

As we conclude this enlightening journey, let us carry forward the knowledge and insights gained, leveraging them to unravel the mysteries of spatial relationships, geometric properties, and the profound interplay between vectors and planes in the captivating realm of 3D space.