Master The Art Of Vector Addition And Subtraction

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Vector addition and subtraction are fundamental operations in the field of mathematics and physics. These concepts play a crucial role in understanding the magnitude and direction of quantities such as force, velocity, and displacement. By mastering the art of vector addition and subtraction, individuals can gain a deeper insight into the principles that govern the physical world.

In essence, vectors are quantities that possess both magnitude and direction. They are represented graphically as arrows, where the length of the arrow corresponds to the magnitude of the vector, and the direction of the arrow indicates the direction of the vector. This visual representation enables us to comprehend complex physical phenomena in a tangible and intuitive manner.

The process of adding vectors involves combining multiple vectors to determine their resultant vector. This resultant vector represents the net effect of the individual vectors acting together. Conversely, vector subtraction entails the removal of one vector from another, yielding a new vector that captures the difference between the two original vectors.

By delving into the realm of vector addition and subtraction, individuals can unlock the ability to analyze and solve real-world problems with precision and clarity. Whether it's calculating the displacement of an object moving in multiple directions or determining the equilibrium of forces acting on an object, these concepts form the cornerstone of many scientific and engineering applications.

In the subsequent sections, we will explore the intricacies of vector addition and subtraction, uncovering the techniques and principles that underpin these operations. Through a comprehensive understanding of these fundamental concepts, individuals can harness the power of vectors to unravel the mysteries of the physical world and make meaningful contributions to various fields of study.

Understanding Vector Addition

Vector addition is the process of combining two or more vectors to determine their resultant vector. In essence, it involves the summation of the individual components of the vectors to obtain a single vector that represents the net effect of the combined vectors. To comprehend vector addition, it is essential to grasp the fundamental properties of vectors and the principles that govern their manipulation.

Vectors possess both magnitude and direction, and they can be represented graphically as arrows. When adding vectors, it is crucial to consider both the magnitude and direction of each vector to accurately determine the resultant vector. The magnitude of a vector is represented by the length of the arrow, while the direction is indicated by the orientation of the arrow.

In the context of vector addition, the components of the vectors are added separately to obtain the resultant vector. This process involves breaking down each vector into its horizontal and vertical components, which are then added together to yield the corresponding components of the resultant vector. By applying the principles of trigonometry and geometry, the magnitude and direction of the resultant vector can be calculated with precision.

One of the key principles governing vector addition is the commutative property, which states that the order of addition does not affect the result. In other words, the resultant vector obtained by adding two vectors remains the same regardless of the order in which the vectors are added. This property simplifies the process of vector addition and allows for greater flexibility in mathematical and physical analyses.

Furthermore, the parallelogram law of vector addition provides a geometric method for determining the resultant vector of two non-parallel vectors. According to this law, the resultant vector is represented by the diagonal of the parallelogram formed by the original vectors. By visualizing the vectors as sides of a parallelogram, individuals can intuitively grasp the concept of vector addition and gain a deeper understanding of the relationship between the original vectors and their resultant.

In summary, understanding vector addition entails a comprehensive grasp of the properties and principles that govern the manipulation of vectors. By leveraging the graphical and mathematical representations of vectors, individuals can master the art of combining vectors to determine their resultant, thereby unlocking the ability to analyze and solve complex problems in mathematics, physics, and various scientific disciplines.

Techniques for Vector Addition

Vector addition encompasses several techniques that facilitate the accurate determination of the resultant vector arising from the combination of multiple vectors. These techniques are essential for manipulating vectors in mathematical and physical contexts, enabling individuals to analyze and solve complex problems with precision.

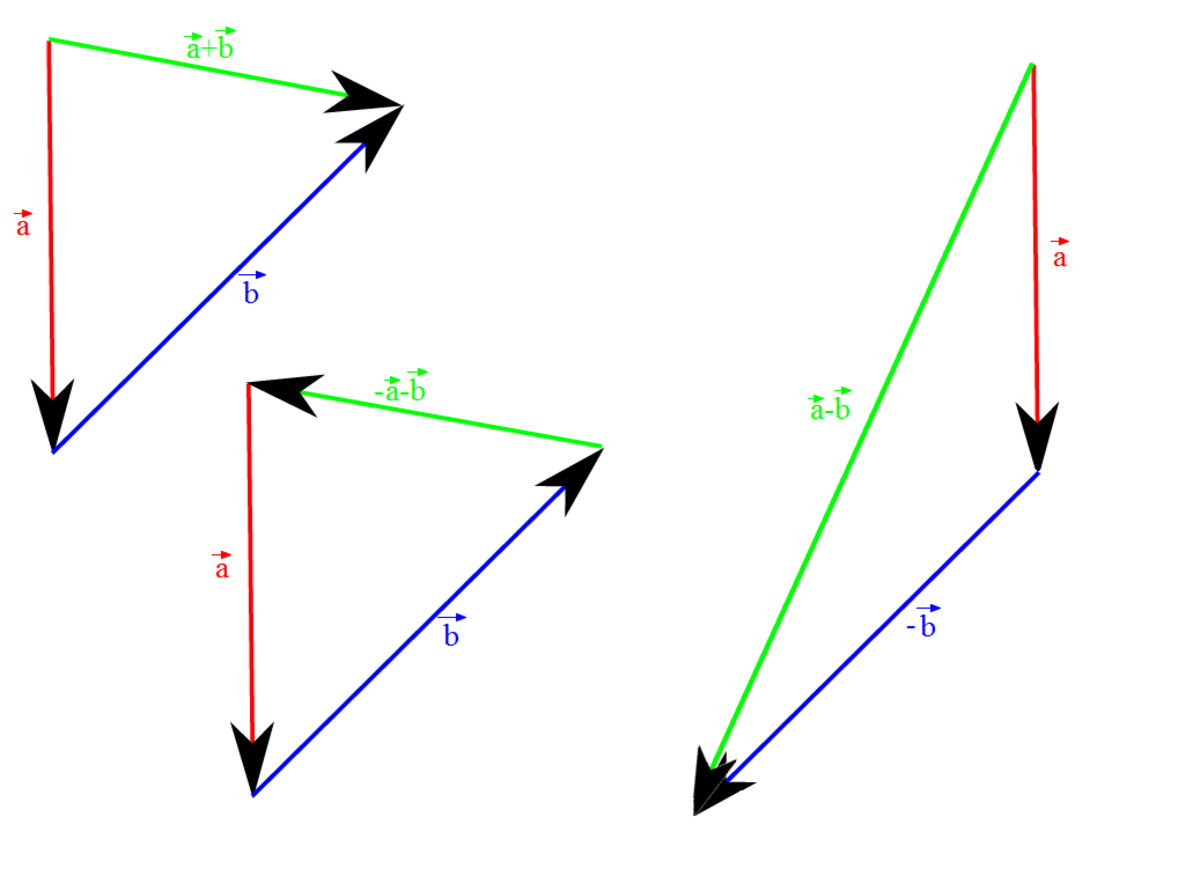
One prominent technique for vector addition is the graphical method, which involves representing vectors as arrows and using geometric principles to determine the resultant vector. By drawing the vectors to scale on a coordinate plane, individuals can visually add the vectors tip-to-tail, creating a closed polygon where the resultant vector is the diagonal. This intuitive approach provides a tangible representation of vector addition, allowing for a clear visualization of the resultant vector's magnitude and direction.

Another technique for vector addition involves resolving vectors into their horizontal and vertical components. By decomposing each vector into its x and y components, individuals can perform separate additions of the horizontal and vertical components to obtain the corresponding components of the resultant vector. This method leverages the principles of trigonometry and basic arithmetic to accurately determine the resultant vector's magnitude and direction.

Additionally, the trigonometric method offers a systematic approach to vector addition by utilizing trigonometric functions such as sine and cosine to calculate the magnitude and direction of the resultant vector. This method is particularly useful when dealing with vectors expressed in polar form, where the magnitude and direction are specified using angle measurements. By applying trigonometric principles, individuals can efficiently add vectors and obtain precise results.

Furthermore, the component method of vector addition involves adding the corresponding components of the vectors to obtain the components of the resultant vector directly. This approach simplifies vector addition by focusing on the individual components of the vectors, allowing for straightforward arithmetic operations to determine the resultant vector's components.

In summary, mastering the techniques for vector addition empowers individuals to manipulate vectors effectively, enabling them to analyze complex physical phenomena and solve mathematical problems with confidence. By leveraging graphical, trigonometric, and component-based methods, individuals can gain a comprehensive understanding of vector addition and harness its power to unravel the mysteries of the physical world.

Understanding Vector Subtraction

Vector subtraction involves the process of determining a new vector that represents the difference between two original vectors. Unlike vector addition, which combines vectors to yield a resultant vector, vector subtraction focuses on isolating the effect of one vector from another, thereby capturing the net effect of their difference. Understanding vector subtraction requires a firm grasp of the properties and principles that govern the manipulation of vectors, as well as the techniques for accurately determining the resultant vector.

When subtracting vectors, it is crucial to consider both the magnitude and direction of the vectors involved. The magnitude of a vector represents its length, while the direction indicates the orientation of the vector. To perform vector subtraction, the components of the vectors are subtracted separately to obtain the corresponding components of the resultant vector. This process involves subtracting the horizontal and vertical components of one vector from the corresponding components of the other vector to yield the components of the resultant vector.

One fundamental principle governing vector subtraction is the concept of adding the opposite. This principle states that subtracting a vector is equivalent to adding the negative of that vector. In mathematical terms, this can be represented as V1 – V2 = V1 + (-V2), where V1 and V2 are the original vectors, and -V2 denotes the negative of vector V2. By applying this principle, individuals can simplify the process of vector subtraction and obtain accurate results by leveraging the techniques and principles of vector addition.

Additionally, the geometric method for vector subtraction involves visualizing the original vectors as arrows and determining the resultant vector by connecting the initial point of the first vector to the terminal point of the second vector. This approach provides a graphical representation of vector subtraction, allowing individuals to intuitively grasp the relationship between the original vectors and their resultant.

By mastering the principles and techniques of vector subtraction, individuals can gain a comprehensive understanding of how vectors interact and influence one another. This understanding is invaluable in various scientific and mathematical applications, enabling individuals to analyze physical phenomena, solve engineering problems, and make informed decisions based on the intricacies of vector subtraction.

Techniques for Vector Subtraction

Vector subtraction encompasses several techniques that enable the precise determination of the resultant vector representing the difference between two original vectors. These techniques play a pivotal role in manipulating vectors in mathematical and physical contexts, providing individuals with the tools to analyze and solve complex problems with accuracy.

One fundamental technique for vector subtraction involves leveraging the principle of adding the opposite. This principle states that subtracting a vector is equivalent to adding the negative of that vector. Mathematically, this can be represented as V1 – V2 = V1 + (-V2), where V1 and V2 are the original vectors, and -V2 denotes the negative of vector V2. By applying this principle, individuals can simplify the process of vector subtraction and obtain accurate results by leveraging the techniques and principles of vector addition.

The geometric method for vector subtraction offers a visual approach to determining the resultant vector representing the difference between two original vectors. By visualizing the original vectors as arrows and connecting the initial point of the first vector to the terminal point of the second vector, individuals can intuitively grasp the relationship between the original vectors and their resultant. This graphical representation provides a tangible insight into the effect of vector subtraction, allowing for a clear visualization of the resultant vector's magnitude and direction.

Furthermore, the component method of vector subtraction involves subtracting the corresponding components of the vectors to obtain the components of the resultant vector directly. This approach simplifies vector subtraction by focusing on the individual components of the vectors, enabling straightforward arithmetic operations to determine the resultant vector's components. By subtracting the horizontal and vertical components of one vector from the corresponding components of the other vector, individuals can accurately determine the components of the resultant vector, thereby capturing the net effect of the vector subtraction.

In summary, mastering the techniques for vector subtraction equips individuals with the ability to manipulate vectors effectively, enabling them to analyze complex physical phenomena and solve mathematical problems with confidence. By leveraging the principles of adding the opposite, the geometric method, and the component method, individuals can gain a comprehensive understanding of vector subtraction and harness its power to unravel the intricacies of the physical world.

Applications of Vector Addition and Subtraction

The concepts of vector addition and subtraction find widespread applications across various scientific, engineering, and mathematical domains, playing a pivotal role in understanding and solving real-world problems. These applications showcase the practical significance and versatility of these fundamental operations, demonstrating their relevance in diverse contexts.

In physics, vector addition and subtraction are instrumental in analyzing forces acting on objects. When multiple forces are exerted on an object from different directions, vector addition allows for the determination of the resultant force, providing crucial insights into the overall effect of the forces. This is particularly valuable in mechanics, where understanding the net force acting on an object is essential for predicting its motion and behavior.

Similarly, in the field of engineering, vector addition and subtraction are indispensable for analyzing complex systems involving multiple forces or velocities. Engineers rely on these operations to calculate the resultant force or velocity in structural analysis, fluid dynamics, and other engineering disciplines. By accurately determining the combined effects of various vectors, engineers can optimize designs, predict system behavior, and ensure the safety and efficiency of engineering projects.

In navigation and geospatial applications, vector addition and subtraction are essential for calculating the displacement and direction of objects or vehicles. For instance, in aviation, the concept of wind correction involves the addition and subtraction of vectors to account for the influence of wind on an aircraft's trajectory. By applying vector addition and subtraction, pilots and navigators can make precise adjustments to ensure accurate navigation and efficient travel.

Moreover, vector addition and subtraction play a crucial role in the field of computer graphics and animation. These operations are used to manipulate the position, orientation, and motion of objects in virtual environments, enabling the creation of realistic and immersive visual simulations. By adding and subtracting vectors representing forces, velocities, or spatial transformations, animators and game developers can achieve lifelike movements and interactions within digital spaces.

Furthermore, in mathematical modeling and optimization, vector addition and subtraction are fundamental for solving systems of equations and optimizing multi-dimensional functions. These operations enable mathematicians and researchers to analyze complex relationships and make informed decisions in various scientific and economic contexts.

In summary, the applications of vector addition and subtraction extend across a wide spectrum of disciplines, encompassing physics, engineering, navigation, computer graphics, mathematics, and beyond. By mastering these fundamental operations, individuals can gain a profound understanding of the physical world, solve intricate problems, and drive innovation across diverse fields of study.

Conclusion

In conclusion, the mastery of vector addition and subtraction is a gateway to understanding and manipulating the fundamental principles that govern the physical world. These operations, rooted in the concept of vectors as quantities with both magnitude and direction, play a pivotal role in various scientific, engineering, and mathematical applications.

By delving into the intricacies of vector addition, individuals gain the ability to combine multiple vectors to determine their resultant vector, providing insights into the net effect of the combined vectors. The principles of commutativity and the parallelogram law, along with graphical and trigonometric techniques, empower individuals to accurately calculate the magnitude and direction of the resultant vector, enabling precise analyses of forces, velocities, and displacements in diverse contexts.

Similarly, the understanding of vector subtraction equips individuals with the tools to isolate the effect of one vector from another, capturing the difference between the original vectors. Leveraging techniques such as adding the opposite and geometric visualization, individuals can accurately determine the resultant vector representing the difference between two original vectors, facilitating analyses of forces, velocities, and spatial transformations in various fields.

The applications of vector addition and subtraction span a wide array of disciplines, including physics, engineering, navigation, computer graphics, and mathematical modeling. From predicting the motion of objects under the influence of multiple forces to optimizing engineering designs and simulating virtual environments with lifelike interactions, these operations form the bedrock of problem-solving and innovation across diverse domains.

In essence, the comprehensive understanding and mastery of vector addition and subtraction empower individuals to unravel the complexities of the physical world, make informed decisions in scientific and engineering endeavors, and drive advancements that shape our understanding of the universe.

Through the exploration of these fundamental operations, individuals can harness the power of vectors to navigate the intricacies of the physical world, solve complex problems with confidence, and pave the way for new discoveries and innovations that transcend the boundaries of human knowledge.