Discover The Secret Formula To Calculate Cone Height Using Volume

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Welcome to the fascinating world of mathematics, where we unravel the secrets of geometric shapes and their intricate properties. Today, we embark on a journey to uncover the hidden formula that allows us to calculate the height of a cone using its volume. This enigmatic formula holds the key to understanding the relationship between the volume and dimensions of a cone, shedding light on its elegant and precise nature.

As we delve into the depths of this mathematical mystery, we will unravel the intricate connections between the volume of a cone and its height. By deciphering the underlying principles and leveraging the power of mathematical reasoning, we will demystify the process of deriving the cone height formula. Through this exploration, we aim to equip you with the knowledge and tools to unlock the potential of this formula, empowering you to solve real-world problems and engage with the beauty of mathematical concepts.

Join us as we embark on this exhilarating quest to unravel the secrets of cone geometry and unveil the hidden formula that bridges the gap between volume and height. Prepare to be captivated by the elegance and precision of mathematical reasoning as we unravel the enigma of cone height calculation. Let's embark on this mathematical odyssey together, where every step brings us closer to unraveling the mysteries of cone geometry and the profound connections between volume and height.

Understanding the Cone Volume Formula

The volume of a cone is a fundamental concept in geometry, representing the amount of space enclosed by this three-dimensional shape. To comprehend the cone volume formula, we must first grasp the defining characteristics of a cone and the principles that govern its volumetric properties.

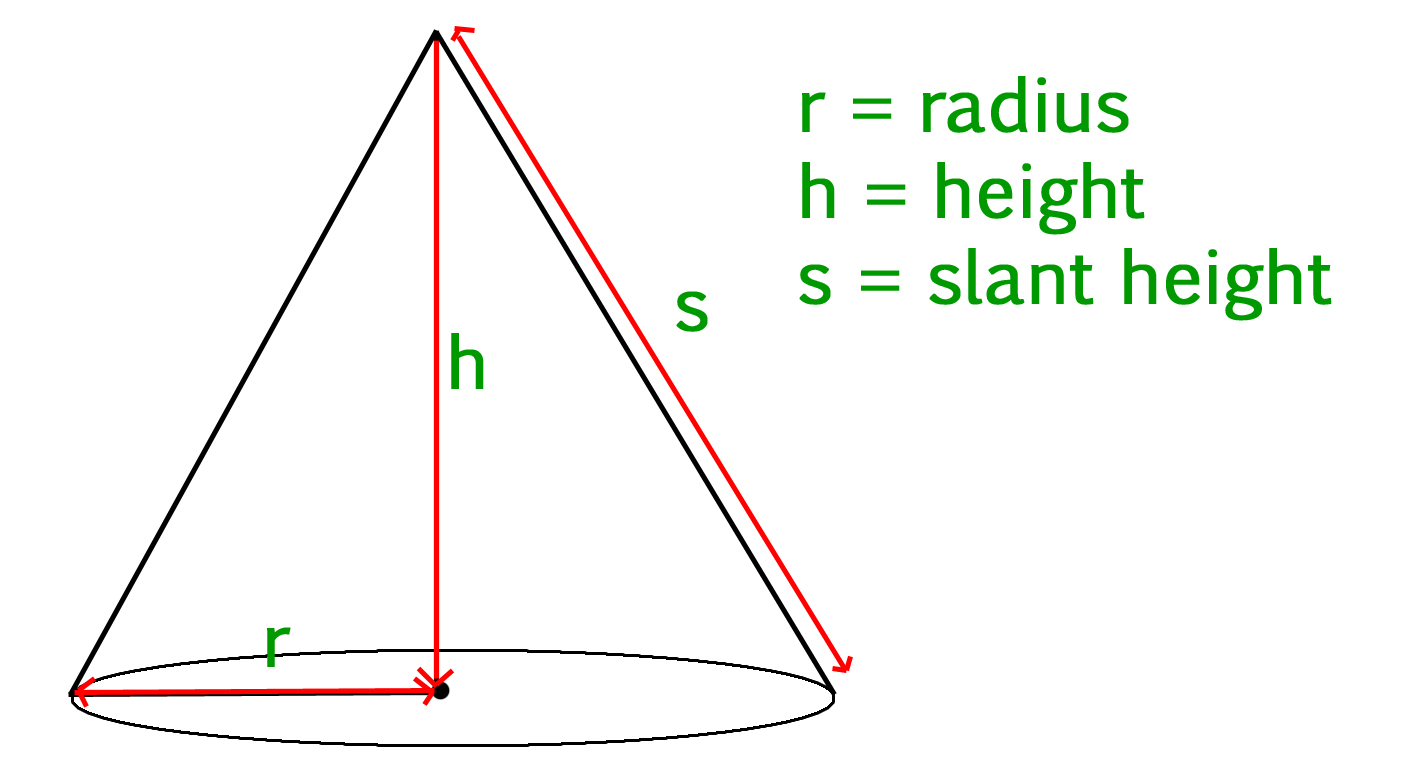
A cone is a geometric solid with a circular base that tapers to a single point, known as the apex. The volume of a cone is calculated using the formula V = (1/3)πr^2h, where V represents the volume, π is a constant approximately equal to 3.14159, r denotes the radius of the base, and h signifies the height of the cone.

The derivation of this formula stems from the concept of geometric similarity and the principles of integral calculus. By envisioning the cone as a series of infinitesimally thin circular discs stacked on top of one another, mathematicians were able to develop a precise method for calculating its volume.

The formula V = (1/3)πr^2h encapsulates the essence of the cone's volumetric properties, illustrating the proportional relationship between the base area, represented by πr^2, and the height of the cone. This elegant formula embodies the symphony of mathematical principles, harmonizing the geometric intricacies of the cone with the power of mathematical reasoning.

Understanding the cone volume formula empowers us to appreciate the intricate balance between the dimensions of the cone and the space it encloses. By unraveling the mathematical underpinnings of this formula, we gain insight into the profound connections between geometry, calculus, and the fundamental principles that govern the physical world.

As we delve deeper into the realm of cone geometry, the volume formula serves as a beacon of understanding, illuminating the path to unlocking the mysteries of this geometric shape. Through this formula, we gain a newfound appreciation for the elegance and precision of mathematical reasoning, as it unveils the hidden symmetries and relationships inherent in the structure of a cone.

In the next section, we will embark on a captivating journey to derive the cone height formula, further enriching our understanding of the intricate connections between volume and dimensions in the realm of cone geometry.

Deriving the Cone Height Formula

The process of deriving the cone height formula is a captivating exploration that unveils the intricate relationship between the volume and dimensions of a cone. By delving into the underlying principles of geometric solids and leveraging the power of mathematical reasoning, we can unravel the enigma of cone height calculation.

To derive the cone height formula, we begin by revisiting the volume formula for a cone, V = (1/3)πr^2h, where V represents the volume, π is a constant approximately equal to 3.14159, r denotes the radius of the base, and h signifies the height of the cone. By rearranging this formula to solve for h, we can isolate the height variable and express it in terms of the cone's volume and base radius.

Through a series of algebraic manipulations, we can transform the volume formula into the form h = 3V / (πr^2), where h represents the height, V denotes the volume, and r signifies the radius of the cone's base. This elegant transformation illuminates the direct relationship between the volume of a cone, the area of its base, and its height.

The derived cone height formula, h = 3V / (πr^2), encapsulates the essence of the volumetric properties of a cone, offering a precise method for calculating its height based on the given volume and base radius. This formula serves as a powerful tool, enabling mathematicians, engineers, and enthusiasts to unlock the secrets of cone geometry and engage with its profound implications.

By deriving the cone height formula, we gain a deeper appreciation for the interconnected nature of geometric shapes and the mathematical principles that govern their properties. This process not only enriches our understanding of cone geometry but also highlights the elegance and precision of mathematical reasoning in unraveling complex relationships.

As we continue our mathematical odyssey, armed with the derived cone height formula, we are poised to apply this newfound knowledge to solve real-world problems and explore the boundless applications of cone geometry. The journey to derive the cone height formula has unveiled the hidden symmetries and connections inherent in the structure of a cone, paving the way for further exploration and discovery in the realm of geometric mathematics.

In the next section, we will harness the power of the derived cone height formula to calculate the height of a cone based on its volume, delving into practical applications that showcase the real-world significance of this mathematical tool.

Applying the Secret Formula to Calculate Cone Height

Armed with the derived cone height formula, h = 3V / (πr^2), we are poised to unlock the practical applications of this mathematical tool and delve into the realm of real-world problem-solving. The process of applying this secret formula to calculate cone height involves leveraging the power of mathematical reasoning to unravel the mysteries of cone geometry and its volumetric properties.

In practical scenarios, the ability to calculate the height of a cone based on its volume is invaluable, especially in fields such as engineering, architecture, and manufacturing. By harnessing the derived cone height formula, engineers and designers can precisely determine the dimensions of cones used in various structures, from industrial tanks and silos to architectural features and geometric sculptures.

Consider a scenario where an engineer is tasked with designing a conical storage vessel with a specific volume requirement. By utilizing the derived cone height formula, the engineer can calculate the necessary height of the vessel to accommodate the desired volume, ensuring optimal space utilization and efficient design. This application showcases the real-world significance of the cone height formula in engineering and design, where precise geometric calculations are essential for achieving functional and practical solutions.

Furthermore, the derived cone height formula serves as a powerful tool for problem-solving in mathematical contexts, allowing students and enthusiasts to engage with the intricacies of cone geometry and volumetric calculations. By applying this formula to a variety of cone-related problems, individuals can deepen their understanding of geometric principles and develop critical thinking skills essential for success in mathematics and related fields.

The application of the cone height formula extends beyond mere calculation, offering a gateway to exploring the profound connections between volume, dimensions, and geometric properties. Through practical exercises and real-world examples, learners can gain a holistic understanding of cone geometry and its practical implications, fostering a deeper appreciation for the elegance and precision of mathematical reasoning.

In essence, applying the secret formula to calculate cone height transcends theoretical abstraction, bringing the beauty and utility of mathematical concepts to the forefront of practical problem-solving. By embracing the derived cone height formula, we embark on a journey of discovery, where the enigmatic properties of cones converge with the power of mathematical reasoning to illuminate the path to understanding and innovation.

As we navigate the realm of cone geometry and its volumetric intricacies, the application of the cone height formula serves as a testament to the enduring relevance and practical significance of mathematical principles in shaping the world around us. Through this application, we unveil the hidden symmetries and connections inherent in the structure of a cone, paving the way for further exploration and discovery in the realm of geometric mathematics.

Conclusion

In conclusion, our journey to unravel the secret formula for calculating cone height using its volume has been a captivating odyssey through the realm of geometric mathematics. We have ventured into the depths of cone geometry, delving into the elegant symmetries and profound connections between volume, dimensions, and the enigmatic properties of this three-dimensional shape. Through our exploration, we have gained a newfound appreciation for the intricate balance between mathematical reasoning and the practical applications of cone geometry in various fields.

The derived cone height formula, h = 3V / (πr^2), stands as a testament to the power of mathematical reasoning in unlocking the mysteries of geometric shapes. This formula serves as a versatile tool, empowering engineers, designers, mathematicians, and enthusiasts to engage with the practical implications of cone geometry and its volumetric properties. By applying this formula to real-world scenarios, we bridge the gap between theoretical abstraction and practical problem-solving, showcasing the enduring relevance of mathematical principles in shaping our understanding of the physical world.

Furthermore, our exploration has illuminated the profound connections between the volume of a cone, the area of its base, and its height. This interconnectedness underscores the elegance and precision of mathematical reasoning, highlighting the inherent symmetries and relationships that define the structure of a cone. By unraveling the enigma of cone height calculation, we have not only enriched our understanding of geometric solids but also cultivated a deeper appreciation for the beauty and utility of mathematical concepts in our daily lives.

As we conclude this mathematical odyssey, we are poised to embark on further explorations, armed with the knowledge and insights gained from our journey. The derived cone height formula serves as a beacon of understanding, guiding us toward new horizons of discovery and innovation in the realm of geometric mathematics. Through our continued engagement with cone geometry and its volumetric intricacies, we are primed to unlock new applications, solve complex problems, and inspire future generations to embrace the elegance and precision of mathematical reasoning.

In essence, the secret formula for calculating cone height using its volume transcends mere mathematical abstraction, offering a gateway to practical insights and real-world significance. Our journey has been a testament to the enduring allure of mathematical reasoning and its profound impact on our understanding of the world. As we bid farewell to this exploration, we carry with us the enduring legacy of mathematical principles, poised to embark on new adventures and unravel the mysteries that shape our mathematical universe.