How To Calculate The Volume Of A Triangular Pyramid

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Calculating the volume of a triangular pyramid is a fundamental concept in geometry and mathematics. It involves understanding the spatial properties of a pyramid with a triangular base and applying a specific formula to determine its volume. This process is not only essential for academic purposes but also has practical applications in fields such as architecture, engineering, and construction.

The volume of a triangular pyramid represents the amount of space enclosed within its four triangular faces and the base. Visualizing this three-dimensional shape can be challenging, but with the right approach, it becomes an intriguing mathematical puzzle to solve. By breaking down the steps involved in calculating the volume, we can demystify the process and gain a deeper appreciation for the beauty of geometric principles.

In this article, we will delve into the intricacies of triangular pyramids, exploring their defining characteristics and the formula used to compute their volume. Through clear explanations and illustrative examples, we will guide you through the step-by-step process of determining the volume of a triangular pyramid. By the end of this journey, you will have a solid grasp of this concept and the confidence to tackle similar geometric challenges with ease.

Understanding the volume of a triangular pyramid opens the door to a world of mathematical exploration and problem-solving. It empowers us to comprehend the spatial relationships between different geometric shapes and equips us with the tools to analyze and manipulate these structures in various contexts. Whether you are a student seeking to deepen your understanding of geometry or a professional aiming to apply mathematical principles in your work, mastering the calculation of a triangular pyramid's volume is a valuable skill with far-reaching implications.

Now, let's embark on this mathematical expedition and unravel the secrets of calculating the volume of a triangular pyramid. Get ready to engage your mind and discover the fascinating world of geometric measurement!

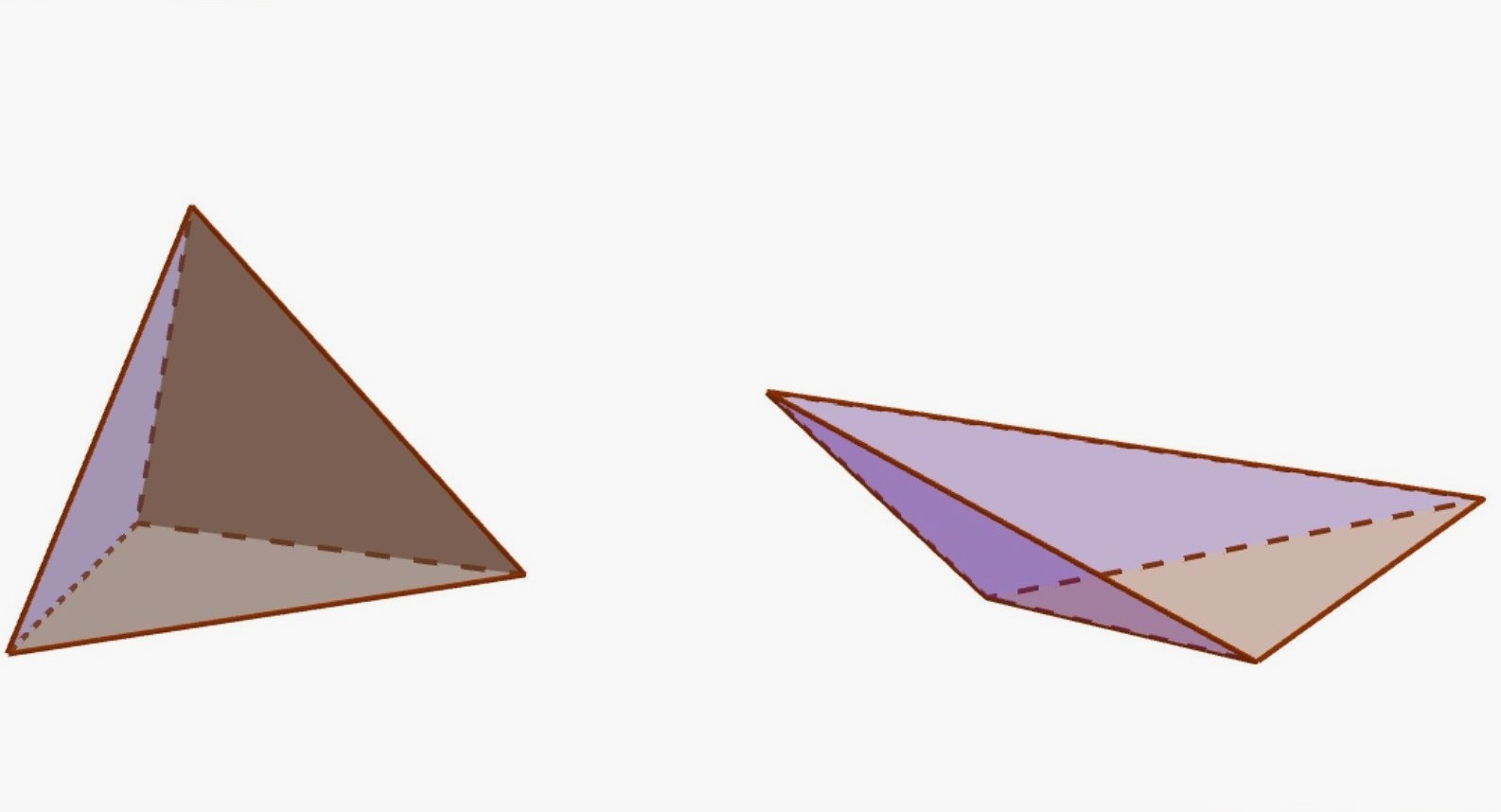
Understanding the Triangular Pyramid

A triangular pyramid, also known as a tetrahedron, is a polyhedron characterized by its four faces, six edges, and four vertices. What sets it apart from other pyramids is its base, which is a triangle, giving the entire structure a distinct geometric profile. This three-dimensional shape exhibits a remarkable symmetry and elegance, making it a captivating subject of study in mathematics and geometry.

The defining feature of a triangular pyramid is its triangular base, which serves as the foundation for the remaining three triangular faces that converge at a single point, known as the apex. This arrangement creates a pyramid with a pointed top, evoking a sense of stability and balance. The triangular base provides a stable platform for the pyramid, while the converging faces contribute to its striking visual appeal and structural integrity.

In addition to its aesthetic allure, the triangular pyramid possesses unique geometric properties that make it a fascinating object of exploration. Its symmetrical nature and well-defined edges and vertices make it an ideal candidate for mathematical analysis and calculation. Understanding the spatial relationships within the triangular pyramid is essential for determining its volume and comprehending its role in various mathematical and practical contexts.

Visualizing the triangular pyramid involves envisioning its triangular base as the starting point, with the three converging faces extending upward to meet at the apex. This spatial arrangement creates a pyramid with distinct height, base, and slant height, all of which play crucial roles in calculating its volume. By grasping the interplay between these geometric elements, we gain a deeper appreciation for the triangular pyramid's structure and its significance in the realm of geometry.

The triangular pyramid's geometric properties extend beyond its visual representation, encompassing fundamental concepts such as surface area, volume, and spatial relationships. These attributes make it a valuable subject for mathematical inquiry and practical applications in fields such as architecture, engineering, and design. By immersing ourselves in the intricacies of the triangular pyramid, we lay the groundwork for mastering its volume calculation and unlocking the potential for further mathematical exploration.

As we delve deeper into the world of triangular pyramids, we will unravel the formula for calculating their volume and embark on a step-by-step journey to demystify this mathematical process. By building a solid understanding of the triangular pyramid's structure and properties, we pave the way for a comprehensive exploration of its volume calculation, empowering us to navigate the complexities of geometric measurement with confidence and clarity.

Formula for Calculating Volume

The volume of a triangular pyramid can be determined using a specific formula that takes into account the dimensions of the pyramid's base and its height. This formula provides a systematic approach to quantifying the amount of space enclosed within the pyramid, offering a precise measurement that is essential for various mathematical and practical applications.

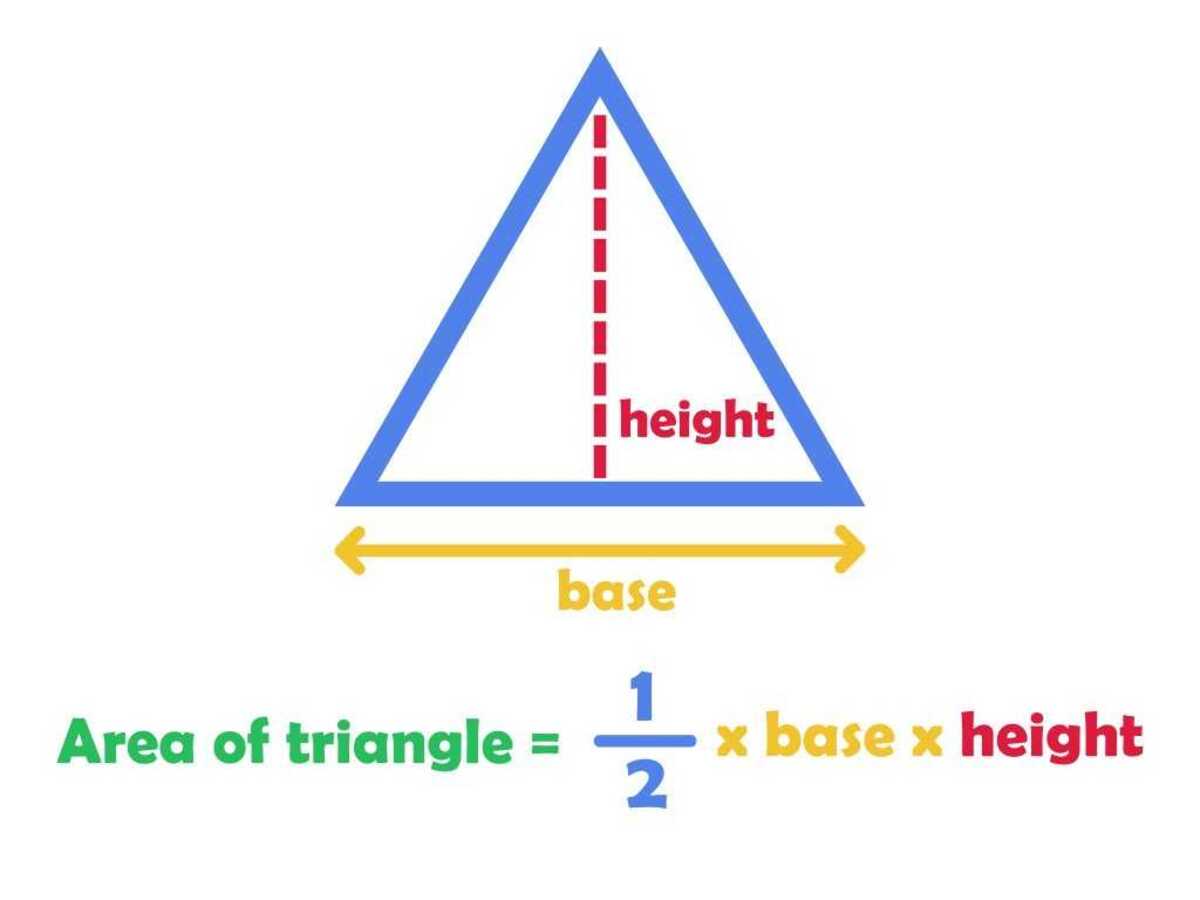
The formula for calculating the volume of a triangular pyramid is derived from the general formula for the volume of a pyramid, which is given by V = (1/3) * B * h, where V represents the volume, B denotes the area of the base, and h signifies the height of the pyramid. For a triangular pyramid, the base area is calculated using the formula for the area of a triangle, which is A = (1/2) * b * h, where A represents the area, b denotes the base length, and h signifies the height of the triangle.

By integrating these formulas, we arrive at the specific formula for calculating the volume of a triangular pyramid, expressed as V = (1/3) * A * H, where V represents the volume, A denotes the area of the triangular base, and H signifies the height of the pyramid. This formula encapsulates the essential geometric parameters required to determine the volume of a triangular pyramid, providing a clear and concise method for mathematical computation.

Understanding the significance of each component in the volume formula is crucial for applying it effectively. The area of the triangular base represents the two-dimensional space enclosed within the base triangle, while the height of the pyramid denotes the perpendicular distance from the base to the apex. By incorporating these measurements into the volume formula, we can accurately quantify the three-dimensional space occupied by the triangular pyramid.

The formula for calculating the volume of a triangular pyramid serves as a foundational tool for geometric measurement and analysis. It enables us to translate the geometric properties of the pyramid into a quantifiable volume, fostering a deeper understanding of spatial relationships and mathematical principles. By mastering this formula, we gain the ability to evaluate and compare the volumes of different triangular pyramids, paving the way for insightful observations and practical applications in diverse fields.

As we delve into the step-by-step calculation of the volume of a triangular pyramid, we will witness the formula in action, unraveling its potential to unlock the mysteries of geometric measurement and empower us to navigate the complexities of spatial analysis with confidence and precision.

Step-by-Step Calculation

Calculating the volume of a triangular pyramid involves a systematic process that integrates the geometric properties of the pyramid's base and height. By following a series of precise steps, we can unravel the volume of the pyramid and gain valuable insights into its spatial characteristics. Let's embark on a step-by-step journey to demystify this mathematical process and witness the formula in action.

1. Determine the Base Area: The first step in calculating the volume of a triangular pyramid is to determine the area of its triangular base. This involves applying the formula for the area of a triangle, which is A = (1/2) * b * h, where A represents the area, b denotes the base length, and h signifies the height of the triangle. By substituting the appropriate values for the base length and height, we can obtain the area of the triangular base.

2. Measure the Height: Next, we need to measure the height of the triangular pyramid, which refers to the perpendicular distance from the base to the apex. This crucial dimension plays a pivotal role in determining the volume of the pyramid, as it directly influences the amount of space enclosed within the structure.

3. Apply the Volume Formula: With the base area and height at our disposal, we can now apply the formula for calculating the volume of a triangular pyramid, expressed as V = (1/3) * A * H, where V represents the volume, A denotes the area of the triangular base, and H signifies the height of the pyramid. By substituting the calculated base area and height into the formula, we can compute the volume of the triangular pyramid.

4. Evaluate the Result: Once the volume is computed, it is essential to evaluate the result in the context of the given problem or scenario. This step involves interpreting the calculated volume in relation to the dimensions of the triangular pyramid and any specific requirements outlined in the problem statement.

By following these step-by-step procedures, we can navigate the intricacies of calculating the volume of a triangular pyramid with precision and clarity. This systematic approach not only reinforces our understanding of geometric measurement but also equips us with the skills to tackle similar mathematical challenges with confidence and proficiency.

As we immerse ourselves in the process of volume calculation, we gain a deeper appreciation for the interplay between geometric dimensions and the systematic application of mathematical formulas. This journey not only enhances our spatial reasoning abilities but also fosters a sense of accomplishment as we unravel the mysteries of geometric measurement and its practical implications.

Example Problems

To solidify our understanding of calculating the volume of a triangular pyramid, let's delve into a series of example problems that showcase the application of the volume formula in diverse scenarios. These problems will not only demonstrate the step-by-step process of volume calculation but also highlight the practical relevance of this mathematical concept in real-world contexts.

Problem 1:

Given:

• Base Length (b): 6 units
• Height of the Triangle Base (h): 4 units
• Height of the Pyramid (H): 10 units

Solution:

1. Determine the Base Area: Using the formula for the area of a triangle, we calculate the area of the triangular base as follows:
   [ A = frac{1}{2} times b times h = frac{1}{2} times 6 times 4 = 12 , text{square units} ]

2. Apply the Volume Formula: Substituting the calculated base area and the height of the pyramid into the volume formula, we obtain the volume of the triangular pyramid:
   [ V = frac{1}{3} times A times H = frac{1}{3} times 12 times 10 = 40 , text{cubic units} ]

3. Evaluation: The volume of the triangular pyramid is 40 cubic units, representing the amount of space enclosed within the pyramid. This result provides a quantitative measure of the pyramid's spatial capacity, essential for various analytical and practical purposes.

Problem 2:

Given:

• Base Length (b): 8 units
• Height of the Triangle Base (h): 5 units
• Height of the Pyramid (H): 12 units

Solution:

1. Determine the Base Area: Applying the formula for the area of a triangle, we calculate the area of the triangular base:
   [ A = frac{1}{2} times b times h = frac{1}{2} times 8 times 5 = 20 , text{square units} ]

2. Apply the Volume Formula: Substituting the calculated base area and the height of the pyramid into the volume formula, we compute the volume of the triangular pyramid:
   [ V = frac{1}{3} times A times H = frac{1}{3} times 20 times 12 = 80 , text{cubic units} ]

3. Evaluation: The volume of the triangular pyramid is 80 cubic units, reflecting the spatial capacity of the pyramid. This quantitative measurement enables us to compare and analyze the volumes of different pyramids, facilitating informed decision-making in various mathematical and practical contexts.

By solving these example problems, we have demonstrated the practical application of the volume formula in determining the spatial capacity of triangular pyramids. These calculations illustrate the systematic approach to geometric measurement and highlight the significance of volume computation in diverse mathematical and real-world scenarios.

Conclusion

In conclusion, the process of calculating the volume of a triangular pyramid is a captivating journey that intertwines geometric principles with mathematical computation. By delving into the spatial properties of the triangular pyramid and unraveling the formula for volume calculation, we have embarked on a profound exploration of geometric measurement and its practical implications.

Throughout this mathematical expedition, we have gained a deeper understanding of the triangular pyramid's structure, its defining characteristics, and the interplay between its base area and height in determining its volume. The step-by-step calculation process has provided us with a systematic approach to unraveling the spatial capacity of the pyramid, reinforcing our spatial reasoning abilities and equipping us with valuable skills for mathematical analysis.

The formula for calculating the volume of a triangular pyramid serves as a foundational tool for geometric measurement, offering a clear and concise method for quantifying the three-dimensional space enclosed within the pyramid. By integrating the area of the triangular base and the height of the pyramid, this formula encapsulates the essential geometric parameters required for volume computation, empowering us to navigate the complexities of spatial analysis with confidence and precision.

Through example problems, we have witnessed the practical application of the volume formula in diverse scenarios, showcasing its relevance in real-world contexts and highlighting its role in facilitating informed decision-making in various mathematical and practical domains. These calculations have not only demonstrated the step-by-step process of volume computation but also underscored the significance of this mathematical concept in spatial analysis and problem-solving.

Mastering the calculation of a triangular pyramid's volume opens the door to a world of mathematical exploration and problem-solving, empowering us to comprehend the spatial relationships between different geometric shapes and equipping us with the tools to analyze and manipulate these structures in various contexts. Whether in academic pursuits or practical applications, the ability to calculate the volume of a triangular pyramid is a valuable skill with far-reaching implications.

As we conclude this mathematical odyssey, we emerge with a newfound appreciation for the beauty of geometric measurement and the profound insights it offers into the spatial dimensions of the world around us. The journey to calculate the volume of a triangular pyramid has not only deepened our understanding of geometry but also instilled in us a sense of wonder and curiosity, fueling our passion for mathematical exploration and discovery.