How To Find Point Of Inflection

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Understanding the concept of points of inflection is crucial in various fields, including mathematics, engineering, and economics. In mathematics, points of inflection play a significant role in analyzing the behavior of functions and determining critical points. These points mark the transition between concave upward and concave downward segments of a curve, providing valuable insights into the shape and characteristics of a function.

Points of inflection are pivotal in understanding the behavior of functions, as they indicate where the curvature of a curve changes. This change in curvature can signify shifts in trends, transitions between growth and decline, or the presence of significant turning points within a given function. By identifying points of inflection, mathematicians and analysts can gain a deeper understanding of the behavior of functions and make informed decisions based on the insights derived from these critical points.

In this comprehensive guide, we will delve into the intricacies of points of inflection, exploring how they are defined, identified, and utilized in mathematical analysis. We will explore the fundamental principles behind points of inflection, the methods for determining them using calculus and graphical analysis, and provide illustrative examples to elucidate their practical significance. By the end of this guide, you will have a clear understanding of how to identify and interpret points of inflection, empowering you to apply this knowledge in various mathematical and analytical contexts.

Understanding Points of Inflection

Points of inflection are critical junctures on the graph of a function where the curvature changes direction. In essence, they mark the transition between concave upward and concave downward segments of a curve. To comprehend points of inflection, it is essential to grasp the concept of concavity.

Concavity refers to the direction in which a curve bends, either upwards or downwards. When a curve is concave upward, it resembles the shape of a cup, with the opening facing upwards. Conversely, when a curve is concave downward, it resembles the shape of a cap, with the opening facing downwards. Points of inflection occur precisely at the points where the concavity changes, signifying a shift in the curvature of the curve.

Mathematically, a point of inflection is characterized by the second derivative of a function. If the second derivative changes sign at a specific point, that point is identified as a point of inflection. When the second derivative changes from positive to negative, the point is a point of inflection, indicating a transition from concave upward to concave downward. Conversely, when the second derivative changes from negative to positive, it also signifies a point of inflection, marking the shift from concave downward to concave upward.

Understanding points of inflection is crucial in analyzing the behavior of functions and identifying critical points that influence the overall shape and characteristics of a curve. By recognizing these pivotal junctures, mathematicians and analysts can gain valuable insights into the trends, turning points, and transitional phases within a function. This knowledge is instrumental in making informed decisions, predicting behavior, and understanding the underlying dynamics of mathematical models and real-world phenomena.

In summary, points of inflection serve as key indicators of changes in curvature within a function, providing essential information about the concavity and overall shape of a curve. By comprehending the significance of these critical points, mathematicians and analysts can unravel the intricate behavior of functions and leverage this understanding to make informed interpretations and strategic decisions based on the insights derived from points of inflection.

Finding Points of Inflection Using Calculus

In calculus, the process of finding points of inflection involves leveraging the principles of differentiation and analyzing the behavior of the second derivative of a function. The second derivative provides crucial information about the concavity of a curve, enabling mathematicians and analysts to pinpoint the exact locations where the curvature changes, thereby identifying points of inflection with precision.

To initiate the process of finding points of inflection using calculus, the first step is to determine the second derivative of the given function. This involves differentiating the function twice with respect to the independent variable. The resulting expression represents the second derivative, which encapsulates essential details about the concavity and curvature of the function.

Once the second derivative is obtained, the next step is to identify the critical points where the second derivative equals zero or is undefined. These critical points serve as potential locations for points of inflection, as they signify the potential transition points between concave upward and concave downward segments of the curve.

After identifying the critical points, the subsequent analysis involves examining the behavior of the second derivative around these points. By evaluating the sign of the second derivative in the intervals surrounding the critical points, it is possible to ascertain the nature of the concavity and determine whether the critical points correspond to actual points of inflection.

If the second derivative changes sign at a critical point, transitioning from positive to negative or vice versa, it indicates the presence of a point of inflection at that specific location. This change in sign signifies the shift in curvature, marking the precise point where the concavity of the curve undergoes a significant transition.

Furthermore, it is essential to verify the concavity of the curve at the identified points of inflection by examining the behavior of the function in the vicinity of these points. This comprehensive analysis ensures the accurate identification of points of inflection and provides a deeper understanding of the curvature dynamics within the function.

By leveraging the power of calculus to analyze the second derivative and its behavior around critical points, mathematicians and analysts can effectively pinpoint the exact locations of points of inflection with mathematical rigor and precision. This methodical approach enables the identification of critical junctures where the curvature changes, empowering individuals to gain profound insights into the behavior and characteristics of functions.

In summary, the process of finding points of inflection using calculus involves leveraging the principles of differentiation and analyzing the behavior of the second derivative to identify critical points and ascertain the presence of points of inflection. This method provides a systematic and rigorous approach to pinpointing the exact locations where the curvature of a curve undergoes significant transitions, facilitating a comprehensive understanding of the behavior of functions and the precise identification of pivotal points within mathematical analysis.

Finding Points of Inflection Using Graphs

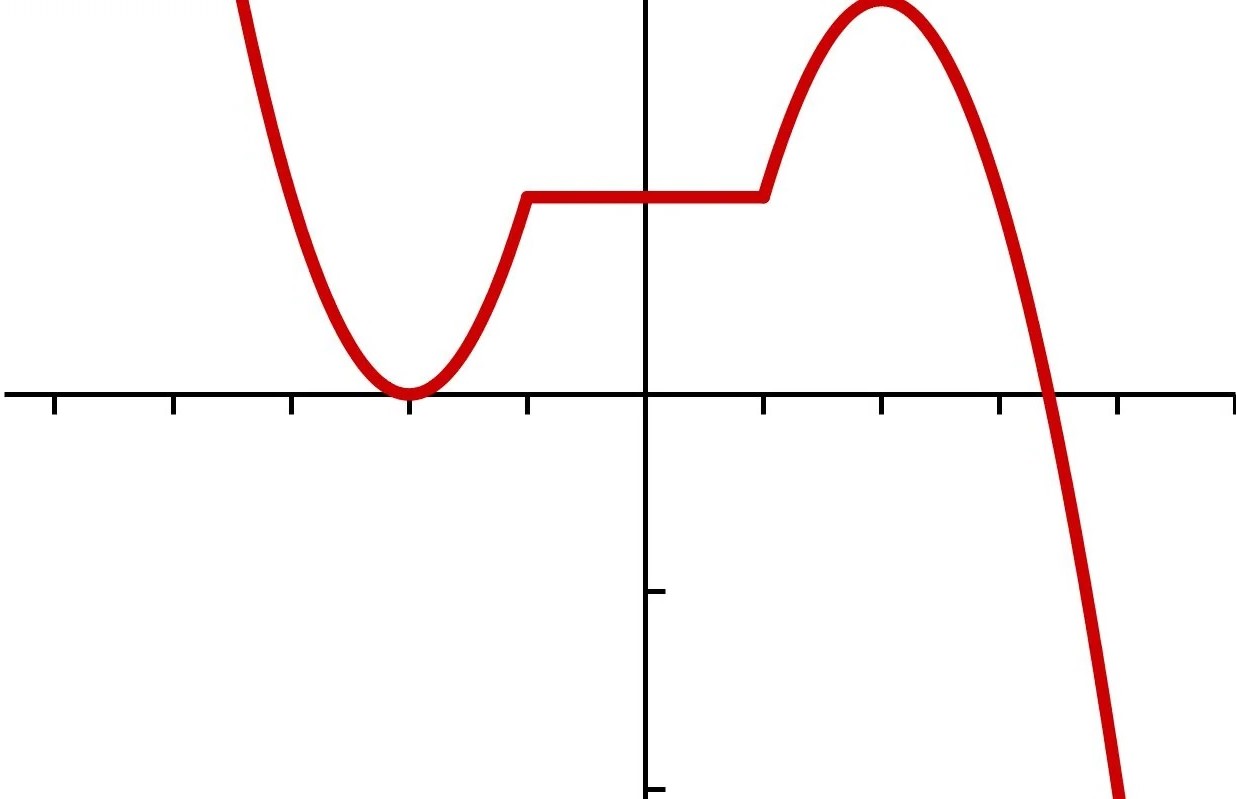
Graphical analysis provides an intuitive and visual approach to identifying points of inflection within the curve of a function. By examining the graph of a function, individuals can discern the concavity and curvature dynamics, enabling them to pinpoint the locations where the curve transitions between concave upward and concave downward segments, thus identifying points of inflection with clarity and insight.

To initiate the process of finding points of inflection using graphs, it is essential to plot the graph of the given function. This visual representation offers a comprehensive view of the curve, showcasing the concave upward and concave downward segments, as well as the potential points of inflection where the curvature changes direction. By visually inspecting the graph, individuals can identify regions where the curve exhibits transitions in concavity, indicating the presence of points of inflection.

One of the key aspects of graphical analysis involves examining the behavior of the curve around critical points, particularly where the concavity appears to change. By focusing on these critical junctures, individuals can observe the curvature of the curve and discern the precise locations where the transition from concave upward to concave downward, or vice versa, occurs. This visual inspection enables the identification of points of inflection based on the distinct changes in the curvature of the curve.

Furthermore, leveraging the graph to analyze the concavity and curvature dynamics facilitates the verification of points of inflection. By visually confirming the transitions in concavity and examining the behavior of the curve at potential points of inflection, individuals can validate the presence of these critical junctures with confidence and precision. This graphical approach provides a tangible and intuitive method for identifying points of inflection, enhancing the understanding of the curvature dynamics within the function.

In summary, the process of finding points of inflection using graphs involves visually analyzing the concavity and curvature transitions within the graph of a function to pinpoint the exact locations where the curve undergoes changes in concavity, thus identifying points of inflection. This graphical approach offers a visual and intuitive method for discerning critical junctures and provides valuable insights into the behavior and characteristics of functions, empowering individuals to comprehend the dynamics of points of inflection with clarity and precision.

Examples of Finding Points of Inflection

To illustrate the practical application of identifying points of inflection, let's consider a quintessential example involving a simple polynomial function. Suppose we have the function f(x) = x^3 – 3x^2 – 9x + 5. Our objective is to determine the points of inflection for this function using both calculus and graphical analysis.

Calculus Approach:

We commence by finding the first and second derivatives of the function f(x). The first derivative, f'(x), is obtained as f'(x) = 3x^2 – 6x – 9. Subsequently, we calculate the second derivative, f''(x), by differentiating f'(x) with respect to x, yielding f''(x) = 6x – 6.

Next, we identify the critical points by setting the second derivative f''(x) equal to zero and solving for x. This yields the critical point x = 1. Therefore, x = 1 represents a potential point of inflection.

To confirm whether x = 1 is indeed a point of inflection, we analyze the behavior of the second derivative around this critical point. By evaluating the sign of the second derivative in the intervals surrounding x = 1, we observe that the sign changes from negative to positive. This change in sign signifies the presence of a point of inflection at x = 1, indicating the transition from concave downward to concave upward.

Graphical Analysis:

Plotting the graph of the function f(x) = x^3 – 3x^2 – 9x + 5 provides a visual representation of the curve. By examining the graph, we can visually identify the regions where the curve exhibits transitions in concavity, indicative of potential points of inflection.

Upon visual inspection, we observe that the curve undergoes a change in concavity around x = 1, where the curvature transitions from concave downward to concave upward. This visual confirmation aligns with our calculus-based analysis, further validating the presence of a point of inflection at x = 1.

In this example, both the calculus approach and graphical analysis converge to identify x = 1 as a point of inflection for the function f(x) = x^3 – 3x^2 – 9x + 5. This demonstration underscores the synergy between mathematical rigor and visual intuition in pinpointing points of inflection, showcasing the practical significance of these critical junctures in analyzing the behavior of functions.

By applying these methodologies to real-world scenarios and complex functions, mathematicians and analysts can leverage the insights derived from points of inflection to make informed interpretations, predict trends, and gain a deeper understanding of the underlying dynamics within mathematical models and analytical frameworks.

This example serves as a testament to the pivotal role of points of inflection in mathematical analysis, highlighting their relevance in unraveling the intricate behavior of functions and their practical implications in diverse fields of study and application.

Conclusion

In conclusion, the concept of points of inflection holds significant importance in mathematical analysis, providing valuable insights into the behavior and characteristics of functions. Through a comprehensive understanding of points of inflection, mathematicians and analysts can unravel the intricate dynamics of curves, discern critical junctures, and make informed interpretations based on the transitions in concavity.

The systematic approaches of finding points of inflection using calculus and graphical analysis offer distinct yet complementary methods for pinpointing these critical junctures within functions. The calculus approach, leveraging the principles of differentiation and the behavior of the second derivative, provides a rigorous and mathematical framework for identifying points of inflection with precision. On the other hand, graphical analysis offers an intuitive and visual method for discerning the transitions in concavity and visually confirming the presence of points of inflection within the graph of a function.

The illustrative example further underscores the practical application of identifying points of inflection, showcasing the synergy between mathematical rigor and visual intuition in pinpointing these critical junctures. By applying these methodologies to real-world scenarios and complex functions, individuals can leverage the insights derived from points of inflection to make informed interpretations, predict trends, and gain a deeper understanding of the underlying dynamics within mathematical models and analytical frameworks.

In essence, points of inflection serve as pivotal indicators of changes in curvature within functions, offering essential information about the concavity and overall shape of curves. By comprehending the significance of these critical points, mathematicians and analysts can gain profound insights into the behavior of functions, empowering them to make informed decisions and strategic interpretations based on the insights derived from points of inflection.

Ultimately, the knowledge and application of points of inflection contribute to a deeper understanding of mathematical models, analytical frameworks, and real-world phenomena, highlighting their relevance in diverse fields of study and application. As individuals continue to explore and leverage the insights derived from points of inflection, they can unlock new perspectives, predict trends, and make informed decisions based on the intricate dynamics of functions and curves.