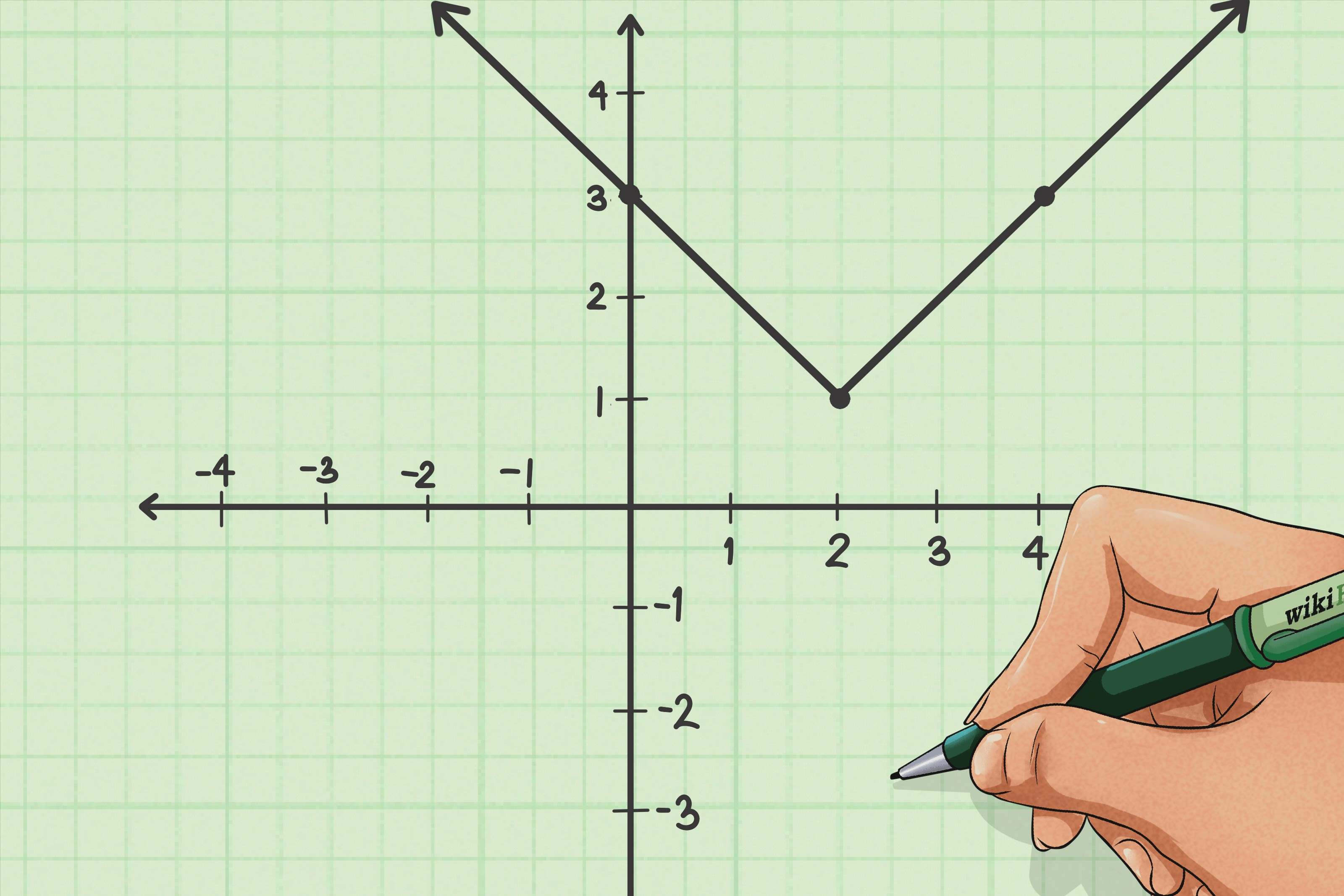How To Perform Reflection Over The X-Axis

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

When it comes to the fascinating world of mathematics, the concept of reflection over the x-axis holds a significant place. This mathematical operation involves transforming a given shape or point across the x-axis, resulting in a mirrored image. Understanding and mastering this fundamental concept not only enriches one's knowledge of geometry and algebra but also lays the groundwork for comprehending more complex mathematical principles.

Reflection over the x-axis is a fundamental transformation in the Cartesian coordinate system. It is a process that involves flipping a shape or point over the x-axis, resulting in a mirrored image. This transformation is crucial in various mathematical applications, including geometry, physics, and computer graphics.

By delving into the intricacies of reflection over the x-axis, we gain a deeper understanding of how shapes and points behave in a coordinate system. This knowledge is not only valuable in academic settings but also finds practical applications in fields such as engineering, architecture, and technology.

In the subsequent sections, we will explore the concept of reflection over the x-axis in detail, unraveling its significance and practical applications. We will delve into the steps involved in performing this transformation, examine examples to illustrate its implementation, and shed light on its real-world relevance. Let's embark on this mathematical journey to uncover the beauty and utility of reflection over the x-axis.

Understanding Reflection Over the x-Axis

Reflection over the x-axis is a fundamental concept in mathematics that involves transforming a shape or point across the x-axis, resulting in a mirrored image. In the Cartesian coordinate system, the x-axis serves as the horizontal reference line, and performing reflection over this axis entails flipping the given shape or point to the opposite side of the x-axis while maintaining the same distance from it. This transformation effectively creates a symmetrical image with respect to the x-axis.

To comprehend reflection over the x-axis, it is essential to grasp the underlying principles of coordinate geometry. In the Cartesian plane, each point is represented by an ordered pair (x, y), where 'x' denotes the horizontal position along the x-axis, and 'y' represents the vertical position along the y-axis. When a shape or point undergoes reflection over the x-axis, the y-coordinate is negated, effectively changing its sign. For instance, if a point has coordinates (x, y), its reflected image will have coordinates (x, -y).

This transformation can also be visualized as a folding of the shape or point along the x-axis, resulting in a perfect reflection across this horizontal line. The distance of each point from the x-axis remains unchanged, but the orientation is inverted, leading to the creation of a symmetrical image.

Understanding reflection over the x-axis is crucial in various mathematical contexts, including geometry, algebra, and trigonometry. It forms the basis for comprehending more advanced transformations and operations in coordinate geometry, paving the way for a deeper understanding of spatial relationships and symmetry.

By mastering the concept of reflection over the x-axis, individuals can gain valuable insights into the behavior of shapes and points in a coordinate system. This knowledge not only enriches their mathematical proficiency but also cultivates a deeper appreciation for the inherent symmetry and structure present in geometric configurations.

In the subsequent sections, we will delve into the practical steps involved in performing reflection over the x-axis, explore illustrative examples, and shed light on its real-world applications, further solidifying the significance of this fundamental mathematical operation.

Steps to Perform Reflection Over the x-Axis

Performing reflection over the x-axis involves a systematic process that allows us to transform a given shape or point across the x-axis, resulting in a mirrored image. This fundamental operation in coordinate geometry is essential for understanding symmetry and spatial transformations. Here are the detailed steps to perform reflection over the x-axis:

1. Identify the Coordinates: Begin by identifying the coordinates of the shape or point that you intend to reflect over the x-axis. In the Cartesian coordinate system, each point is represented by an ordered pair (x, y), where 'x' denotes the horizontal position and 'y' represents the vertical position.

2. Negate the y-Coordinate: To reflect a point over the x-axis, negate the y-coordinate of the given point. This means that if the original point has coordinates (x, y), the reflected point will have coordinates (x, -y). This step is crucial in achieving the mirrored image across the x-axis.

3. Apply the Transformation to Each Point: If you are dealing with a shape composed of multiple points, apply the reflection transformation to each individual point. By negating the y-coordinate of each point, you effectively mirror the entire shape across the x-axis, creating a symmetrical image.

4. Visualize the Mirrored Image: Once the reflection transformation is applied to the coordinates, visualize the resulting mirrored image. This involves observing the new positions of the points after the reflection over the x-axis. The reflected shape will appear as a symmetrical image with respect to the x-axis.

5. Verify the Symmetry: After performing the reflection, verify the symmetry of the mirrored image with respect to the x-axis. Check if the distance of each point from the x-axis remains unchanged, while the orientation is inverted. This validation step ensures the accuracy of the reflection transformation.

By following these systematic steps, one can effectively perform reflection over the x-axis, creating mirrored images of shapes and points in the Cartesian coordinate system. Mastering this process not only enhances one's understanding of coordinate geometry but also lays the foundation for comprehending more advanced transformations and spatial operations.

In the subsequent section, we will explore illustrative examples of reflection over the x-axis, further elucidating the practical application of these steps in real-world mathematical scenarios.

Examples of Reflection Over the x-Axis

To illustrate the concept of reflection over the x-axis, let's delve into a few compelling examples that showcase the practical application of this fundamental transformation in coordinate geometry.

Example 1: Reflecting a Single Point

Consider the point A with coordinates (3, 4) in the Cartesian plane. To perform reflection over the x-axis, we negate the y-coordinate, resulting in the reflected point A' with coordinates (3, -4). Visually, this transformation flips the point A across the x-axis, creating a mirrored image below the original position. This simple example demonstrates the fundamental principle of reflection over the x-axis, where the x-coordinate remains unchanged, while the y-coordinate is negated to produce the mirrored image.

Example 2: Reflecting a Line Segment

Let's examine a line segment defined by the points P(2, 3) and Q(2, 6) in the Cartesian plane. By applying the reflection transformation to each point, we obtain the reflected segment P'(2, -3) and Q'(2, -6) across the x-axis. This results in a mirrored image of the original line segment, showcasing the symmetrical nature of reflection over the x-axis. The distance of each point from the x-axis remains unchanged, emphasizing the preservation of spatial relationships during the transformation.

Example 3: Reflecting a Geometric Shape

Now, let's consider a geometric shape, such as a triangle with vertices at points A(4, 5), B(6, 7), and C(8, 3) in the Cartesian plane. Applying the reflection transformation to each vertex yields the reflected triangle with vertices A'(4, -5), B'(6, -7), and C'(8, -3) across the x-axis. This transformation results in a perfectly mirrored image of the original triangle, highlighting the symmetrical arrangement of the reflected vertices with respect to the x-axis.

Example 4: Reflecting a Complex Figure

For a more intricate example, let's envision a complex figure composed of multiple points in the Cartesian plane. By systematically applying the reflection transformation to each point, we can observe the creation of a symmetrical image across the x-axis. This example underscores the versatility of reflection over the x-axis, demonstrating its applicability to diverse shapes and configurations in coordinate geometry.

By exploring these examples, we gain valuable insights into the practical implementation of reflection over the x-axis. This fundamental transformation not only facilitates the creation of mirrored images but also enriches our understanding of symmetry and spatial relationships in the Cartesian coordinate system. These examples serve as compelling illustrations of the real-world relevance and significance of reflection over the x-axis in mathematical contexts.

In the subsequent section, we will delve into the applications of reflection over the x-axis, shedding light on its diverse uses in various fields beyond pure mathematics.

Applications of Reflection Over the x-Axis

Reflection over the x-axis holds significant practical applications across various fields, leveraging its fundamental principles to solve real-world problems and facilitate essential transformations. The versatility of this mathematical operation extends beyond pure mathematics, finding relevance in diverse domains such as engineering, architecture, physics, and computer graphics.

In engineering and architecture, reflection over the x-axis plays a crucial role in designing and analyzing structures. By employing this transformation, engineers and architects can create symmetrical blueprints and models, ensuring balance and stability in their designs. This application is particularly valuable in the construction of bridges, buildings, and other architectural marvels, where symmetry and structural integrity are paramount.

In the realm of physics, reflection over the x-axis is instrumental in understanding the behavior of light and sound waves. When light or sound waves encounter a reflective surface, they undergo a transformation akin to reflection over the x-axis, leading to the creation of mirrored images. This phenomenon is fundamental in optics and acoustics, forming the basis for the design of mirrors, lenses, and acoustic reflectors.

Moreover, reflection over the x-axis finds extensive use in computer graphics and digital imaging. Graphic designers and software developers utilize this transformation to create visually appealing and symmetrical graphics, animations, and user interfaces. By incorporating reflection over the x-axis into their design processes, they can achieve balanced and aesthetically pleasing visual compositions.

In the context of mathematical modeling and data analysis, reflection over the x-axis is employed to study symmetrical patterns and relationships. This application is particularly relevant in statistical analysis and curve fitting, where understanding the symmetrical distribution of data points is essential for making informed decisions and predictions.

Furthermore, reflection over the x-axis plays a pivotal role in the study of symmetry and transformations in mathematics education. By introducing students to this fundamental concept, educators can foster a deeper understanding of spatial relationships and geometric properties, laying the groundwork for advanced mathematical explorations.

Overall, the applications of reflection over the x-axis extend far beyond its theoretical underpinnings, permeating various disciplines and contributing to the advancement of knowledge and innovation. By recognizing the practical relevance of this fundamental transformation, we gain a deeper appreciation for its pervasive influence in the world around us.

Conclusion

In conclusion, the concept of reflection over the x-axis stands as a fundamental pillar in the realm of coordinate geometry, offering profound insights into symmetry, spatial transformations, and practical applications across diverse fields. Through our exploration of this fundamental mathematical operation, we have unraveled its significance and practical relevance, shedding light on its role in shaping our understanding of spatial relationships and geometric configurations.

By delving into the intricacies of reflection over the x-axis, we have gained a deeper appreciation for the symmetrical nature of this transformation and its impact on the Cartesian coordinate system. The systematic steps involved in performing reflection over the x-axis have provided a clear roadmap for creating mirrored images of shapes and points, emphasizing the preservation of spatial relationships and the inherent symmetry present in geometric configurations.

The illustrative examples presented have vividly demonstrated the real-world application of reflection over the x-axis, showcasing its versatility in transforming individual points, line segments, geometric shapes, and complex figures. These examples have underscored the practical utility of this transformation in diverse fields, ranging from engineering and architecture to physics, computer graphics, and mathematical modeling.

Furthermore, our exploration of the applications of reflection over the x-axis has revealed its pervasive influence in various domains, including engineering, architecture, physics, computer graphics, and mathematics education. This transformation serves as a cornerstone for creating balanced designs, understanding wave behavior, developing visually appealing graphics, analyzing data patterns, and fostering a deeper understanding of symmetry in educational settings.

In essence, reflection over the x-axis transcends its theoretical foundations, permeating the fabric of our physical and digital worlds. Its role in fostering symmetry, balance, and structural integrity underscores its indispensable nature in diverse applications, enriching our understanding of spatial transformations and geometric principles.

As we conclude our journey through the intricacies of reflection over the x-axis, we are reminded of its enduring significance in shaping our perception of symmetry, spatial relationships, and the inherent beauty of geometric configurations. This fundamental concept not only enriches our mathematical proficiency but also resonates across various disciplines, leaving an indelible mark on the way we perceive and interact with the world around us.