How To Tell If A Relation Is A Function

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Understanding the concept of relations and functions is fundamental in mathematics. In the realm of mathematics, a relation is a set of ordered pairs, while a function is a specific type of relation. The distinction between the two lies in the way the elements of the domain are related to the elements of the codomain. This distinction is crucial in various mathematical applications, from algebra to calculus and beyond.

In this article, we will delve into the intricacies of relations and functions, exploring how to differentiate between the two. By the end of this discussion, you will have a clear understanding of how to determine if a given relation is indeed a function. This knowledge will empower you to navigate mathematical problems with confidence and precision.

Let's embark on this enlightening journey through the world of relations and functions, unraveling the mysteries and unveiling the methods to discern whether a relation qualifies as a function. Through practical examples and insightful explanations, we will equip you with the tools to tackle this fundamental concept in mathematics. So, let's dive in and explore the fascinating realm of relations and functions, demystifying their intricacies along the way.

Understanding Relations and Functions

In the realm of mathematics, relations and functions play a pivotal role in understanding the connections between sets of elements. A relation is essentially a set of ordered pairs, where the first element in each pair is related to the second element. This relationship can take various forms, such as equality, inequality, or other mathematical operations. On the other hand, a function is a specific type of relation in which each element in the domain is uniquely paired with an element in the codomain.

To comprehend the distinction between relations and functions, it is essential to grasp the concept of domain and codomain. The domain of a relation or function consists of all the input values, while the codomain encompasses all the possible output values. In a function, each element in the domain maps to exactly one element in the codomain, distinguishing it from a general relation where this one-to-one correspondence may not hold true.

Furthermore, functions exhibit a key property known as the vertical line test. This test dictates that for a relation to be a function, no vertical line passing through the graph of the relation should intersect the graph more than once. This criterion ensures that each input value (x-coordinate) corresponds to a unique output value (y-coordinate), thereby affirming the function's one-to-one mapping.

In contrast, a relation that fails the vertical line test signifies a violation of the one-to-one correspondence between the domain and codomain, thus disqualifying it as a function. Understanding this fundamental principle is crucial in discerning whether a given relation qualifies as a function.

In summary, the distinction between relations and functions lies in the nature of their mappings from the domain to the codomain. While relations encompass a broad spectrum of connections between elements, functions adhere to a stricter criterion of one-to-one correspondence. By comprehending this distinction and the associated properties, one can effectively discern whether a given relation constitutes a function, thereby laying the foundation for more advanced mathematical analyses and applications.

Testing for Functions

Determining whether a given relation qualifies as a function entails employing various tests and methods to scrutinize its properties. These tests serve as powerful tools to ascertain the one-to-one correspondence between the elements of the domain and codomain, a hallmark of functions in mathematics.

Using the Vertical Line Test

The vertical line test stands as a fundamental criterion for evaluating whether a relation is a function. This test involves visually inspecting the graph of the relation and ensuring that no vertical line intersects the graph at more than one point. If the graph passes this test, it signifies that each input value (x-coordinate) uniquely corresponds to an output value (y-coordinate), thereby meeting the essential criterion of a function. Conversely, if a vertical line intersects the graph at multiple points, the relation fails the vertical line test, indicating a violation of the one-to-one mapping characteristic of functions.

Using the Horizontal Line Test

In addition to the vertical line test, the horizontal line test provides another method to assess the nature of a relation. This test involves examining the graph of the relation to ensure that no horizontal line intersects the graph at more than one point. If the graph passes this test, it reinforces the one-to-one correspondence between the domain and codomain, affirming the function's unique mapping. Conversely, if a horizontal line intersects the graph at multiple points, it signifies a breach of the one-to-one mapping criterion, thus disqualifying the relation as a function.

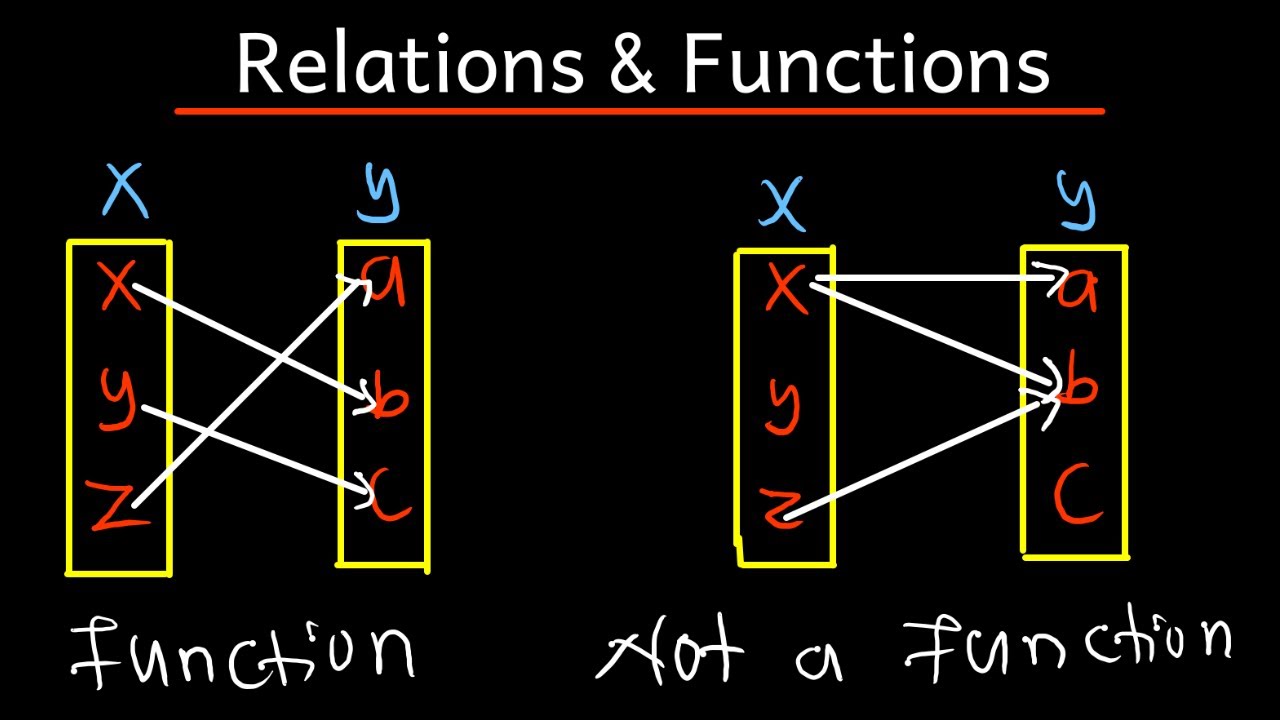
Using the Mapping Diagram

Another approach to test for functions involves constructing a mapping diagram to visually represent the relation between the domain and codomain. By systematically pairing each element in the domain with its corresponding element in the codomain, one can discern whether each domain element uniquely maps to a codomain element. If every domain element has a unique mapping, the relation satisfies the one-to-one correspondence criterion, establishing it as a function. Conversely, if any domain element maps to multiple codomain elements, it indicates a violation of the function's essential property, rendering the relation non-functional.

By employing these rigorous tests and methods, one can effectively evaluate whether a given relation qualifies as a function. These techniques not only serve as powerful tools for mathematical analysis but also deepen one's understanding of the fundamental principles that underpin the concept of functions in mathematics.

Using the Vertical Line Test

The vertical line test serves as a fundamental criterion for evaluating whether a relation qualifies as a function. This test provides a visual method to scrutinize the graph of a relation and ascertain its adherence to the one-to-one correspondence between the elements of the domain and codomain, a defining characteristic of functions in mathematics.

When applying the vertical line test, one visually inspects the graph of the relation and ensures that no vertical line intersects the graph at more than one point. This visual inspection is crucial in determining whether each input value (x-coordinate) uniquely corresponds to an output value (y-coordinate), thereby meeting the essential criterion of a function. If the graph passes this test, it signifies that the relation adheres to the one-to-one mapping characteristic, affirming its status as a function.

Conversely, if a vertical line intersects the graph at multiple points, the relation fails the vertical line test. This failure indicates a violation of the one-to-one mapping criterion, thereby disqualifying the relation as a function. Such an outcome underscores the significance of the vertical line test in discerning the nature of a relation and its qualification as a function.

The visual nature of the vertical line test not only provides a practical method for evaluating functions but also offers a tangible representation of the one-to-one correspondence between the domain and codomain. By observing the behavior of vertical lines in relation to the graph, one gains insight into the unique mapping of input values to output values, a fundamental aspect of functions in mathematics.

In summary, the vertical line test stands as a powerful tool for assessing whether a given relation constitutes a function. Its visual approach not only facilitates the identification of functions but also deepens one's understanding of the essential properties that distinguish functions from general relations. Through the application of the vertical line test, one can effectively discern the one-to-one correspondence between the elements of the domain and codomain, thereby illuminating the fundamental concept of functions in mathematics.

Using the Horizontal Line Test

The horizontal line test serves as a valuable method for evaluating the nature of a relation and determining its qualification as a function. This test provides a visual and analytical approach to scrutinize the graph of a relation, shedding light on its adherence to the one-to-one correspondence between the elements of the domain and codomain, a fundamental characteristic of functions in mathematics.

When applying the horizontal line test, one examines the graph of the relation to ensure that no horizontal line intersects the graph at more than one point. This visual inspection is pivotal in ascertaining whether each output value (y-coordinate) uniquely corresponds to an input value (x-coordinate), thereby meeting the essential criterion of a function. If the graph passes this test, it signifies that the relation adheres to the one-to-one mapping characteristic, affirming its status as a function.

Conversely, if a horizontal line intersects the graph at multiple points, the relation fails the horizontal line test. This failure indicates a breach of the one-to-one mapping criterion, thereby disqualifying the relation as a function. Such an outcome underscores the significance of the horizontal line test in discerning the nature of a relation and its qualification as a function.

The visual and analytical nature of the horizontal line test not only provides a practical method for evaluating functions but also offers a tangible representation of the one-to-one correspondence between the domain and codomain. By observing the behavior of horizontal lines in relation to the graph, one gains insight into the unique mapping of output values to input values, a fundamental aspect of functions in mathematics.

In summary, the horizontal line test stands as a powerful tool for assessing whether a given relation constitutes a function. Its visual and analytical approach not only facilitates the identification of functions but also deepens one's understanding of the essential properties that distinguish functions from general relations. Through the application of the horizontal line test, one can effectively discern the one-to-one correspondence between the elements of the domain and codomain, thereby illuminating the fundamental concept of functions in mathematics.

Using the Mapping Diagram

The mapping diagram serves as a valuable tool for visually representing the relation between the domain and codomain, providing a systematic approach to discern whether a given relation qualifies as a function. This method offers a tangible and structured representation of the one-to-one correspondence between the elements of the domain and codomain, a fundamental characteristic of functions in mathematics.

To employ the mapping diagram, one systematically pairs each element in the domain with its corresponding element in the codomain, creating a visual mapping that elucidates the relationship between the input and output values. By meticulously constructing this diagram, one can effectively evaluate whether each domain element uniquely maps to a codomain element, thereby meeting the essential criterion of a function.

The mapping diagram not only offers a visual representation of the relation but also provides a comprehensive overview of the one-to-one correspondence between the domain and codomain. Each domain element is meticulously linked to its corresponding codomain element, showcasing the unique mapping characteristic that distinguishes functions from general relations.

By scrutinizing the mapping diagram, one gains insight into the nature of the relation and its adherence to the one-to-one mapping criterion. If every domain element has a unique mapping to the codomain, the relation satisfies the essential property of a function, thereby affirming its qualification as a function. Conversely, if any domain element maps to multiple codomain elements, it indicates a violation of the function's fundamental property, rendering the relation non-functional.

In summary, the mapping diagram provides a structured and visual approach to evaluating whether a given relation constitutes a function. Its systematic representation of the relationship between the domain and codomain not only facilitates the identification of functions but also deepens one's understanding of the essential properties that distinguish functions from general relations. Through the application of the mapping diagram, one can effectively discern the one-to-one correspondence between the elements of the domain and codomain, thereby illuminating the fundamental concept of functions in mathematics.

Conclusion

In conclusion, the distinction between relations and functions lies in the nature of their mappings from the domain to the codomain. While relations encompass a broad spectrum of connections between elements, functions adhere to a stricter criterion of one-to-one correspondence. Throughout this exploration, we have delved into the intricacies of relations and functions, unraveling the methods to discern whether a given relation qualifies as a function.

By understanding the fundamental principles and employing rigorous tests such as the vertical line test, horizontal line test, and mapping diagram, one can effectively evaluate whether a given relation constitutes a function. These tests not only serve as powerful tools for mathematical analysis but also deepen one's understanding of the essential properties that underpin the concept of functions in mathematics.

The visual and analytical nature of these tests provides practical methods for evaluating functions and offers tangible representations of the one-to-one correspondence between the domain and codomain. By observing the behavior of vertical and horizontal lines in relation to the graph, and by systematically pairing each element in the domain with its corresponding element in the codomain, one gains insight into the unique mapping of input and output values, a fundamental aspect of functions in mathematics.

Ultimately, the ability to discern whether a given relation qualifies as a function is crucial in various mathematical applications, from algebra to calculus and beyond. This knowledge empowers individuals to navigate mathematical problems with confidence and precision, laying the foundation for more advanced mathematical analyses and applications.

In essence, the journey through the world of relations and functions has equipped us with the tools to tackle this fundamental concept in mathematics. By comprehending the distinction between relations and functions and the associated properties, one can effectively discern whether a given relation constitutes a function, thereby illuminating the fundamental concept of functions in mathematics.