How To Tell If A Function Is Even Or Odd

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Understanding the nature of functions is fundamental in mathematics, as it provides insights into their behavior and properties. One key aspect of functions is whether they are even, odd, or neither. This distinction plays a crucial role in various mathematical applications, including calculus, algebra, and trigonometry. In this article, we will delve into the concept of even and odd functions, exploring their definitions, characteristics, and methods for determining their nature.

The identification of even and odd functions is essential for analyzing symmetry and patterns within mathematical models. By discerning whether a function exhibits even symmetry, odd symmetry, or neither, mathematicians can gain valuable information about its behavior and graphical representation. This knowledge serves as a cornerstone for solving equations, graphing functions, and understanding the fundamental properties of mathematical relationships.

Throughout this article, we will explore the distinct features of even and odd functions, providing clear explanations and practical examples to illustrate their significance. By the end of this discussion, readers will have a comprehensive understanding of how to identify and differentiate between even and odd functions, empowering them to apply this knowledge in various mathematical contexts. Let's embark on this enlightening journey into the world of even and odd functions, unraveling their mysteries and unveiling their profound implications in the realm of mathematics.

Definition of Even and Odd Functions

In mathematics, functions are classified as even, odd, or neither based on their symmetry and behavior. Understanding the definitions of even and odd functions is crucial for analyzing their properties and graphical representations.

An even function is defined as a function for which the value of f(x) is equal to f(-x) for all x in the function's domain. In simpler terms, this means that the function is symmetric with respect to the y-axis. Visually, an even function's graph exhibits reflection symmetry across the y-axis, where the right half of the graph mirrors the left half. This symmetry implies that the function produces identical outputs for opposite inputs, resulting in a graph that is indistinguishable when reflected across the y-axis.

On the other hand, an odd function is characterized by the property that f(x) equals -f(-x) for all x in the function's domain. This definition signifies that the function displays rotational symmetry of 180 degrees around the origin. Graphically, an odd function's plot possesses rotational symmetry, where rotating the graph 180 degrees around the origin yields an identical shape. Consequently, the outputs of an odd function for opposite inputs have opposite signs, leading to a graph that maintains its form when rotated by 180 degrees.

It is important to note that a function can also be classified as neither even nor odd if it does not satisfy the criteria for even or odd functions. In such cases, the function may exhibit no specific symmetry with respect to the y-axis or the origin, leading to a unique pattern that does not align with the characteristics of even or odd functions.

By comprehending the definitions of even and odd functions, mathematicians can discern the distinct symmetrical properties exhibited by different types of functions. This understanding serves as a foundational element for analyzing functions, determining their behavior, and interpreting their graphical representations. As we proceed, we will explore the methods for testing whether a function is even or odd, further solidifying our grasp of these fundamental concepts in mathematics.

Testing for Even Functions

To determine whether a function is even, mathematicians employ a straightforward yet powerful method known as the even function test. This test involves substituting -x for x in the function and comparing the result with the original function. If the function's value remains unchanged after this substitution, it is classified as an even function.

Mathematically, this test can be expressed as follows: for a function f(x) to be even, it must satisfy the condition f(x) = f(-x) for all x in its domain. This criterion signifies that the function's output for a given input x is equivalent to its output for the opposite input -x, indicating symmetry across the y-axis.

Practically, when testing for even functions, mathematicians substitute -x for x in the function and evaluate whether the resulting expression matches the original function. If the two expressions are equal, the function is confirmed to be even. This verification process provides a clear and definitive way to ascertain the even nature of a function.

Furthermore, the graphical representation of even functions serves as a visual confirmation of their symmetry. The symmetric nature of even functions is evident in their graphs, which exhibit reflection symmetry across the y-axis. This graphical characteristic aligns with the algebraic test for even functions, reinforcing the understanding of their symmetrical properties.

In essence, the process of testing for even functions involves both algebraic and graphical analyses, enabling mathematicians to confidently determine whether a function possesses even symmetry. By applying the even function test and examining the graphical representation, mathematicians can effectively identify and classify functions based on their symmetrical properties, laying the groundwork for deeper insights into their behavior and characteristics.

As we delve into the realm of even functions, it becomes evident that the testing process provides a robust framework for discerning the symmetrical nature of functions, offering a systematic approach to categorizing and understanding their fundamental properties. This methodical approach equips mathematicians with the tools to unravel the mysteries of even functions, paving the way for comprehensive analyses and applications in various mathematical contexts.

Testing for Odd Functions

Determining whether a function is odd involves a distinct set of criteria and tests that unveil its unique symmetrical properties. An odd function test serves as the cornerstone for identifying functions that exhibit rotational symmetry around the origin, a defining characteristic of odd functions.

The fundamental principle underlying the test for odd functions is rooted in the property that defines their symmetry. Mathematically, for a function f(x) to be classified as odd, it must satisfy the condition f(x) = -f(-x) for all x in its domain. This criterion signifies that the function's output for a given input x is equal to the negation of its output for the opposite input -x, indicating rotational symmetry of 180 degrees around the origin.

Practically, when testing for odd functions, mathematicians substitute -x for x in the function and evaluate whether the resulting expression is the negation of the original function. If the two expressions are equal in magnitude but opposite in sign, the function is confirmed to be odd. This algebraic test provides a clear and definitive method for ascertaining the odd nature of a function, offering a systematic approach to discerning its symmetrical properties.

Graphically, odd functions exhibit distinct characteristics that align with their rotational symmetry around the origin. The graphical representation of odd functions displays symmetry with respect to the origin, where rotating the graph 180 degrees yields an identical shape. This visual confirmation of rotational symmetry reinforces the understanding of odd functions and complements the algebraic test, providing a comprehensive means of identifying and classifying functions based on their symmetrical properties.

In essence, the process of testing for odd functions encompasses both algebraic and graphical analyses, enabling mathematicians to confidently determine whether a function possesses rotational symmetry around the origin. By applying the odd function test and examining the graphical representation, mathematicians can effectively identify and classify functions based on their unique symmetrical properties, paving the way for deeper insights into their behavior and characteristics.

As we delve into the realm of odd functions, it becomes evident that the testing process provides a robust framework for discerning the symmetrical nature of functions, offering a systematic approach to categorizing and understanding their fundamental properties. This methodical approach equips mathematicians with the tools to unravel the mysteries of odd functions, paving the way for comprehensive analyses and applications in various mathematical contexts.

Examples of Even and Odd Functions

To solidify our understanding of even and odd functions, let's explore concrete examples that vividly illustrate their distinct properties and symmetrical characteristics. By delving into these examples, we can gain valuable insights into the behavior and graphical representations of even and odd functions, further enhancing our comprehension of these fundamental concepts in mathematics.

Example 1: Even Function

Consider the function f(x) = x^2, a classic example of an even function. Applying the even function test, we substitute -x for x in the function:
f(-x) = (-x)^2 = x^2

Upon comparison with the original function f(x) = x^2, we observe that f(-x) yields the same result as f(x), satisfying the condition for even functions. Graphically, the plot of f(x) = x^2 exhibits reflection symmetry across the y-axis, with the right half mirroring the left half. This symmetrical nature confirms the even property of the function, as it produces identical outputs for opposite inputs, exemplifying the hallmark characteristics of even functions.

Example 2: Odd Function

Let's examine the function g(x) = x^3, a quintessential representation of an odd function. Applying the odd function test, we substitute -x for x in the function:
g(-x) = (-x)^3 = -x^3

Upon comparison with the original function g(x) = x^3, we observe that g(-x) yields the negation of g(x), satisfying the condition for odd functions. Graphically, the plot of g(x) = x^3 displays rotational symmetry of 180 degrees around the origin, where rotating the graph yields an identical shape. This distinctive symmetry confirms the odd property of the function, as it produces outputs with opposite signs for opposite inputs, exemplifying the characteristic features of odd functions.

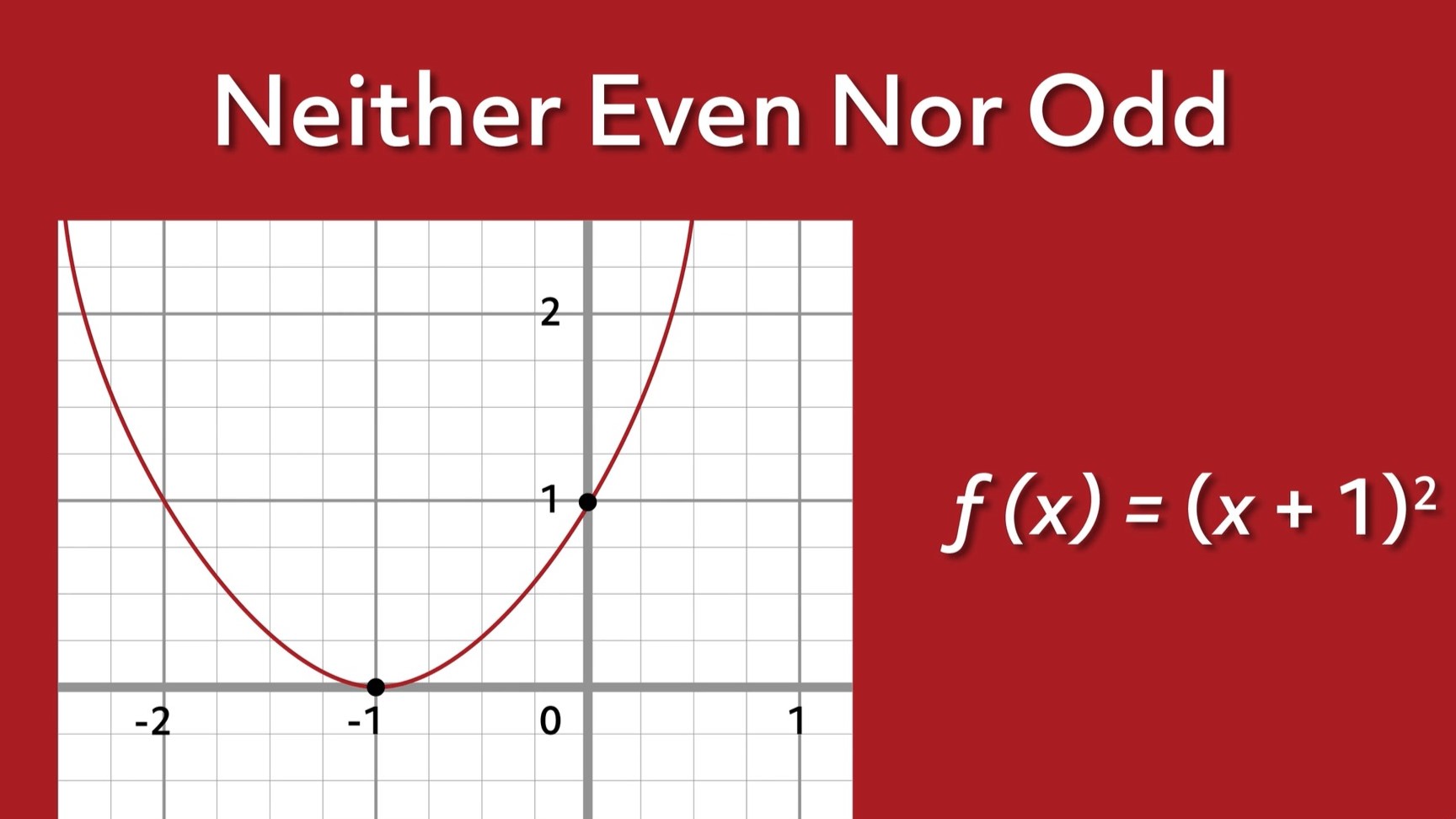
Example 3: Neither Even nor Odd

Now, let's consider the function h(x) = x^2 + x, which does not satisfy the criteria for even or odd functions. Upon applying the even function test, we find that h(-x) does not yield the same result as h(x), and applying the odd function test reveals that h(-x) does not yield the negation of h(x). Graphically, the plot of h(x) = x^2 + x does not exhibit clear reflection symmetry across the y-axis or rotational symmetry around the origin, indicating that it does not align with the characteristics of even or odd functions.

By examining these examples, we gain a deeper appreciation for the distinct properties and symmetrical behaviors of even and odd functions. These concrete illustrations elucidate the algebraic and graphical manifestations of even and odd functions, providing valuable insights into their fundamental nature and paving the way for their application in diverse mathematical contexts.

This exploration of examples reinforces our understanding of even and odd functions, equipping us with the knowledge to discern and categorize functions based on their symmetrical properties. As we continue to unravel the intricacies of mathematical functions, these examples serve as guiding beacons, illuminating the profound implications of even and odd functions in the realm of mathematics.

Conclusion

In conclusion, the concept of even and odd functions holds significant importance in the realm of mathematics, offering valuable insights into the symmetrical properties and behaviors of functions. Through our exploration, we have gained a comprehensive understanding of the definitions, testing methods, and graphical representations of even and odd functions, paving the way for their practical application in various mathematical contexts.

The identification and classification of even and odd functions provide mathematicians with a powerful framework for analyzing symmetry, patterns, and graphical representations within mathematical models. By discerning whether a function exhibits even symmetry, odd symmetry, or neither, mathematicians can glean crucial information about its behavior and properties. This knowledge serves as a cornerstone for solving equations, graphing functions, and interpreting the fundamental characteristics of mathematical relationships.

The testing methods for even and odd functions, encompassing algebraic analyses and graphical verifications, offer a systematic approach to discerning the symmetrical nature of functions. The even function test, which involves substituting -x for x and comparing the results, provides a clear and definitive method for ascertaining the even nature of a function. Similarly, the odd function test, rooted in the property that defines rotational symmetry around the origin, offers a robust framework for identifying functions that exhibit this unique characteristic.

Furthermore, the concrete examples of even and odd functions have illuminated their distinct properties and symmetrical behaviors, providing valuable insights into their fundamental nature. The graphical representations of these functions vividly illustrate their reflective and rotational symmetries, reinforcing our comprehension of their symmetrical properties and enhancing our ability to discern and categorize functions based on these characteristics.

As we conclude our exploration of even and odd functions, it becomes evident that this knowledge serves as a fundamental building block for deeper insights into the behavior and properties of mathematical functions. By unraveling the mysteries of even and odd functions, mathematicians are equipped with the tools to analyze and interpret the symmetrical properties of functions, laying the groundwork for their application in diverse mathematical contexts.

In essence, the understanding of even and odd functions empowers mathematicians to delve into the intricacies of mathematical models, uncovering symmetrical patterns and behaviors that underpin a wide array of mathematical phenomena. This knowledge not only enriches our comprehension of functions but also serves as a springboard for further explorations and applications in the dynamic landscape of mathematics.