How To Find Perpendicular Slope

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Understanding the concept of perpendicular slope is crucial in various mathematical and real-world applications. When dealing with lines and angles, the perpendicular slope plays a significant role in determining the relationship between two intersecting lines. In this article, we will delve into the fundamentals of slope and explore the method for finding the perpendicular slope of a given line.

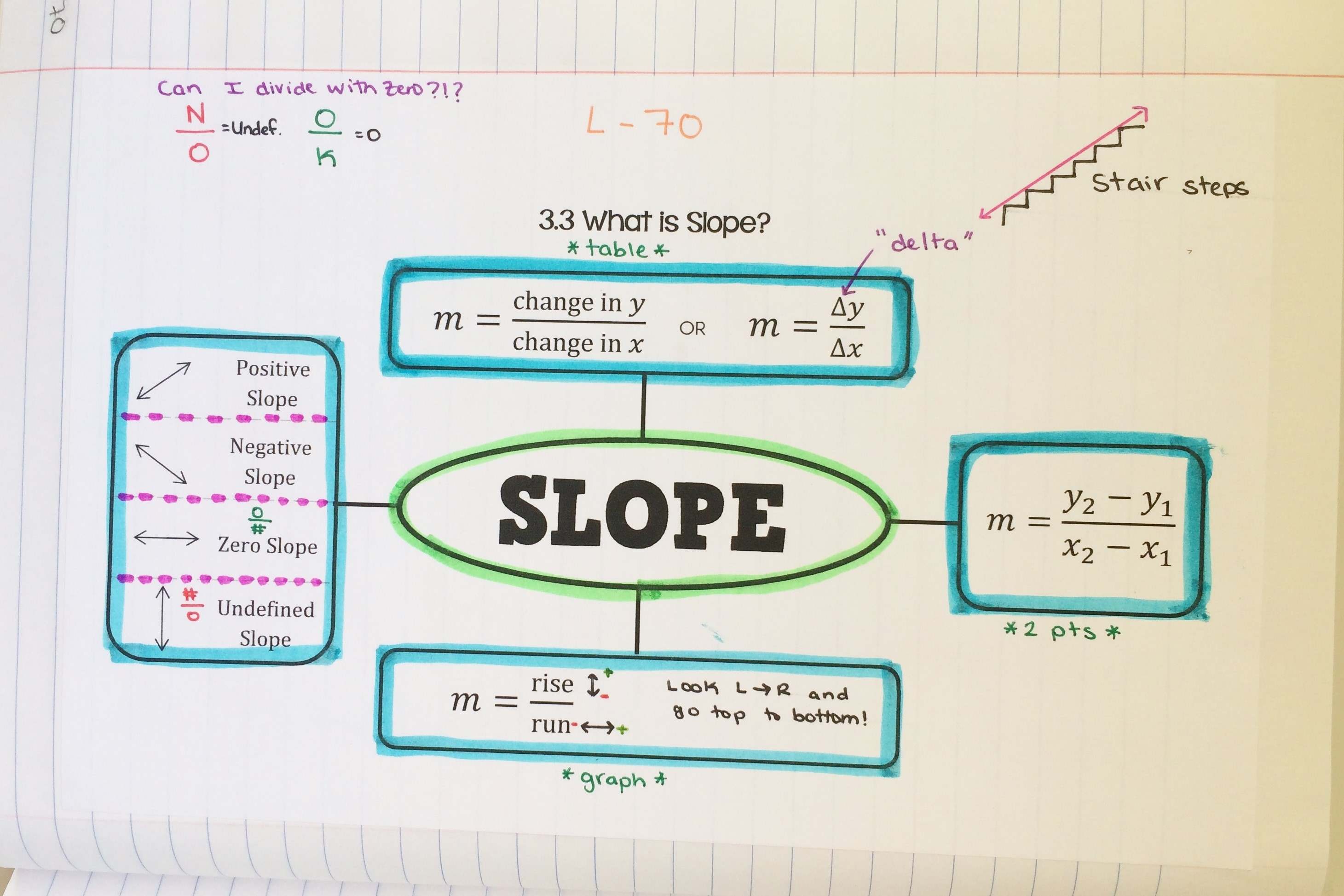
The concept of slope represents the measure of the steepness of a line. It is a fundamental aspect of linear equations and is expressed as the ratio of the vertical change (rise) to the horizontal change (run) between two distinct points on the line. The slope is denoted by the letter "m" and can be positive, negative, zero, or undefined, depending on the orientation of the line.

When two lines are perpendicular, they intersect at a 90-degree angle, forming an "L" shape. In this scenario, the slopes of the two lines are negative reciprocals of each other. This means that if the slope of one line is "m," the slope of the perpendicular line will be "-1/m." Understanding this relationship is essential for various mathematical problems, such as determining the slope of a line that is perpendicular to a given line or finding the equation of a line that is perpendicular to another line at a specific point.

Throughout this article, we will explore the step-by-step process of finding the perpendicular slope, providing clear examples to illustrate the concept. By mastering this fundamental principle, you will gain a deeper understanding of the relationships between lines and angles, paving the way for enhanced problem-solving skills in mathematics and beyond. Let's embark on this journey to unravel the intricacies of perpendicular slope and its significance in the world of mathematics.

Understanding Slope

Slope is a fundamental concept in mathematics, particularly in the study of linear equations and geometry. It measures the steepness of a line and provides crucial insights into the relationship between two points on a line. The slope, denoted by the letter "m," is calculated as the ratio of the vertical change (rise) to the horizontal change (run) between two distinct points on the line. This fundamental relationship is expressed in the slope formula as:

[ m = frac{y_2 – y_1}{x_2 – x_1} ]

Here, ((x_1, y_1)) and ((x_2, y_2)) represent the coordinates of the two points on the line. The slope formula allows us to quantify the rate at which the line rises or falls as it progresses horizontally.

The slope can take various forms, each conveying specific characteristics of the line. A positive slope indicates that the line rises as it progresses from left to right, while a negative slope signifies a descent in the same direction. A slope of zero represents a horizontal line, indicating no vertical change between points, and an undefined slope corresponds to a vertical line, signifying no horizontal change.

Understanding slope is crucial in analyzing the behavior of linear equations and their graphical representations. It provides valuable information about the direction and steepness of a line, enabling us to make predictions and solve various mathematical problems. Moreover, slope serves as a foundational concept in calculus, physics, engineering, and other disciplines, where the rate of change and gradients are essential considerations.

In summary, the concept of slope forms the bedrock of linear relationships and geometric interpretations. By comprehending the significance of slope and its implications in different contexts, we can gain a deeper appreciation for the fundamental principles that underpin mathematical reasoning and problem-solving.

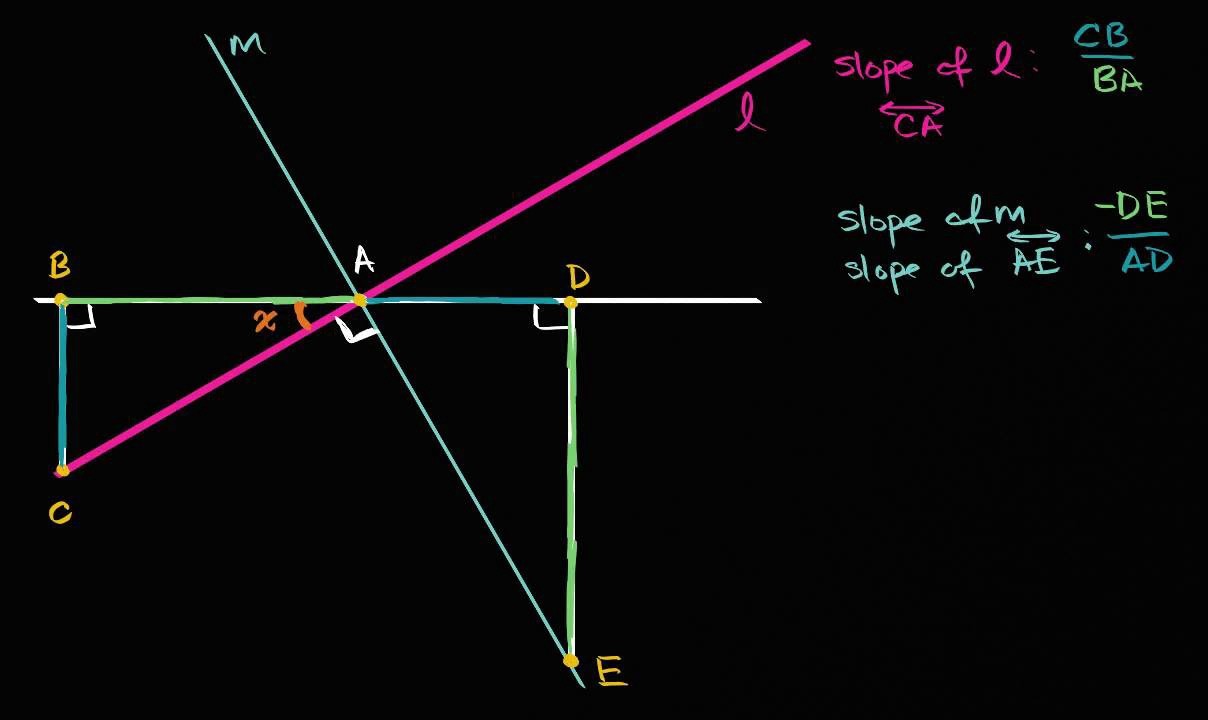
Finding the Perpendicular Slope

When dealing with intersecting lines, the concept of perpendicular slope becomes a crucial element in understanding their relationship. Finding the perpendicular slope involves determining the slope of a line that is perpendicular to a given line. This process is guided by a fundamental principle: the slopes of perpendicular lines are negative reciprocals of each other. In other words, if the slope of one line is represented by "m," the slope of the perpendicular line will be "-1/m."

To find the perpendicular slope of a given line, we first calculate the slope of the original line using the slope formula: [ m = frac{y_2 – y_1}{x_2 – x_1} ]. Once we have the slope "m" of the original line, we can then apply the concept of negative reciprocal to determine the perpendicular slope. This involves taking the negative reciprocal of the original slope, which is expressed as "-1/m."

For example, if the slope of a given line is 2, the perpendicular slope would be -1/2. Similarly, if the original slope is -3/4, the perpendicular slope would be 4/3. This relationship holds true for all pairs of perpendicular lines, providing a straightforward method for determining the perpendicular slope based on the slope of the original line.

Understanding the process of finding the perpendicular slope is essential in various mathematical applications, particularly in geometry and coordinate geometry. It enables us to identify the orientation of perpendicular lines and establish their geometric properties. Moreover, this concept plays a vital role in solving problems related to angles, line intersections, and the graphical representation of linear equations.

By mastering the technique of finding the perpendicular slope, individuals can enhance their problem-solving skills and gain a deeper understanding of the geometric relationships between lines. This foundational knowledge serves as a building block for more advanced concepts in mathematics and provides a solid framework for analyzing spatial configurations and geometric patterns.

In summary, the process of finding the perpendicular slope involves calculating the original slope of a line and then applying the concept of negative reciprocal to determine the slope of the perpendicular line. This fundamental principle forms the basis for understanding the relationship between intersecting lines and is instrumental in various mathematical contexts, contributing to a comprehensive grasp of geometric concepts and analytical reasoning.

Examples of Finding Perpendicular Slope

To further solidify our understanding of finding perpendicular slope, let's explore a few illustrative examples that demonstrate the application of this fundamental concept in mathematics.

Example 1: Calculating Perpendicular Slope from Given Line

Suppose we have a line with the equation y = 3x + 2. To find the perpendicular slope of this line, we begin by identifying the slope of the original line. The given equation is in the form y = mx + b, where 'm' represents the slope. In this case, the slope of the line is 3.

To determine the perpendicular slope, we apply the concept of negative reciprocal. By taking the negative reciprocal of the original slope, we obtain -1/3 as the perpendicular slope. Therefore, the line perpendicular to y = 3x + 2 has a slope of -1/3.

Example 2: Finding Perpendicular Slope from Coordinates

Consider two points A(2, 5) and B(4, 9) on a line. To find the perpendicular slope of the line passing through these points, we first calculate the slope using the formula: [ m = frac{y_2 – y_1}{x_2 – x_1} ]. Substituting the coordinates of points A and B, we get:

m = [ frac{9 – 5}{4 – 2} ] = [ frac{4}{2} ] = 2

The slope of the original line passing through points A and B is 2. To find the perpendicular slope, we apply the concept of negative reciprocal. The perpendicular slope is -1/2, obtained by taking the negative reciprocal of the original slope.

Example 3: Perpendicular Slope in Real-world Context

In a practical scenario, consider a ramp with a slope of 1/4, representing the rise over run. To ensure accessibility for individuals with mobility aids, such as wheelchairs, it is essential to construct a perpendicular ramp with a slope that is the negative reciprocal of the original ramp's slope.

By applying the concept of negative reciprocal, the perpendicular ramp should have a slope of -4/1, which simplifies to -4. This ensures that the perpendicular ramp is inclined at a steeper angle, facilitating safe and convenient access for individuals with mobility challenges.

These examples vividly illustrate the practical application of finding perpendicular slope in various mathematical contexts, emphasizing its significance in determining the orientation and relationships between intersecting lines. By mastering this fundamental concept, individuals can enhance their problem-solving skills and gain a deeper understanding of geometric principles in both theoretical and real-world scenarios.

In summary, the process of finding perpendicular slope involves calculating the original slope of a line and then applying the concept of negative reciprocal to determine the slope of the perpendicular line. This foundational knowledge serves as a building block for analyzing spatial configurations and geometric patterns, contributing to a comprehensive grasp of mathematical concepts and analytical reasoning.

Conclusion

In conclusion, the concept of perpendicular slope holds immense significance in the realm of mathematics, particularly in the study of lines, angles, and geometric relationships. Through our exploration of finding the perpendicular slope, we have unveiled a fundamental principle that governs the orientation and interplay of intersecting lines. By understanding the relationship between the slopes of perpendicular lines, individuals can gain valuable insights into the geometric properties and spatial configurations that underpin various mathematical problems and real-world scenarios.

The process of finding the perpendicular slope involves calculating the original slope of a line and then applying the concept of negative reciprocal to determine the slope of the perpendicular line. This foundational knowledge serves as a building block for analyzing spatial configurations and geometric patterns, contributing to a comprehensive grasp of mathematical concepts and analytical reasoning.

Moreover, the practical examples presented in this article showcase the diverse applications of finding perpendicular slope, ranging from determining the orientation of ramps to solving geometric problems based on coordinate geometry. By mastering this fundamental concept, individuals can enhance their problem-solving skills and gain a deeper understanding of the geometric relationships between lines, paving the way for enhanced spatial reasoning and analytical thinking.

The ability to identify perpendicular slopes not only enriches one's mathematical toolkit but also fosters a deeper appreciation for the interconnectedness of mathematical concepts and their real-world implications. Whether in the context of architectural design, engineering, or spatial analysis, the concept of perpendicular slope serves as a guiding principle for understanding the relationships between intersecting lines and their implications in diverse fields.

In essence, the journey to unravel the intricacies of perpendicular slope has equipped us with a foundational understanding of a fundamental geometric concept. By mastering the technique of finding the perpendicular slope, individuals can enhance their problem-solving skills and gain a deeper appreciation for the fundamental principles that underpin mathematical reasoning and spatial relationships. This knowledge serves as a springboard for further exploration of geometric concepts and their applications in diverse disciplines, empowering individuals to navigate the complexities of spatial configurations and geometric patterns with confidence and proficiency.