How To Find The Slope Of A Tangent Line

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Understanding the concept of tangent lines and how to find their slope is a fundamental aspect of mathematics, particularly in the realm of calculus. Tangent lines play a crucial role in understanding the behavior of curves and functions, making them a key component of mathematical analysis and problem-solving.

In this article, we will delve into the intricacies of tangent lines, exploring how they relate to curves and how their slopes can be determined. By the end of this discussion, you will have a clear understanding of how to find the slope of a tangent line and its significance in the context of calculus.

Tangent lines are like the secret agents of the mathematical world, stealthily touching curves at a single point and revealing valuable information about the behavior of functions. They provide a snapshot of a curve's steepness at a specific point, offering insights into its instantaneous rate of change. This makes them indispensable tools for understanding the dynamic nature of functions and their derivatives.

As we embark on this journey, we will unravel the mystery behind tangent lines, uncovering their role in calculus and real-world applications. By grasping the concept of tangent lines and mastering the art of finding their slopes, you will gain a deeper appreciation for the elegance and precision of mathematical analysis.

So, fasten your seatbelts and get ready to explore the fascinating world of tangent lines and their slopes. Whether you're a math enthusiast, a student navigating the complexities of calculus, or simply someone intrigued by the beauty of mathematical concepts, this exploration will equip you with the knowledge and skills to conquer the enigmatic realm of tangent lines. Let's dive in and unravel the secrets of finding the slope of a tangent line!

Understanding Tangent Lines

Tangent lines are like the undercover agents of the mathematical world, stealthily touching curves at a single point and revealing valuable information about the behavior of functions. In the realm of calculus, these elusive lines play a pivotal role in understanding the dynamic nature of curves and functions. But what exactly are tangent lines, and why are they so significant?

Imagine a roller coaster ride through the intricate twists and turns of a mathematical curve. At any given point along the ride, the roller coaster's path is governed by the steepness of the track, dictating the speed and intensity of the journey. Similarly, a tangent line to a curve represents the instantaneous steepness or slope of the curve at a specific point. It's as if the tangent line whispers secrets about the curve's behavior at that precise location.

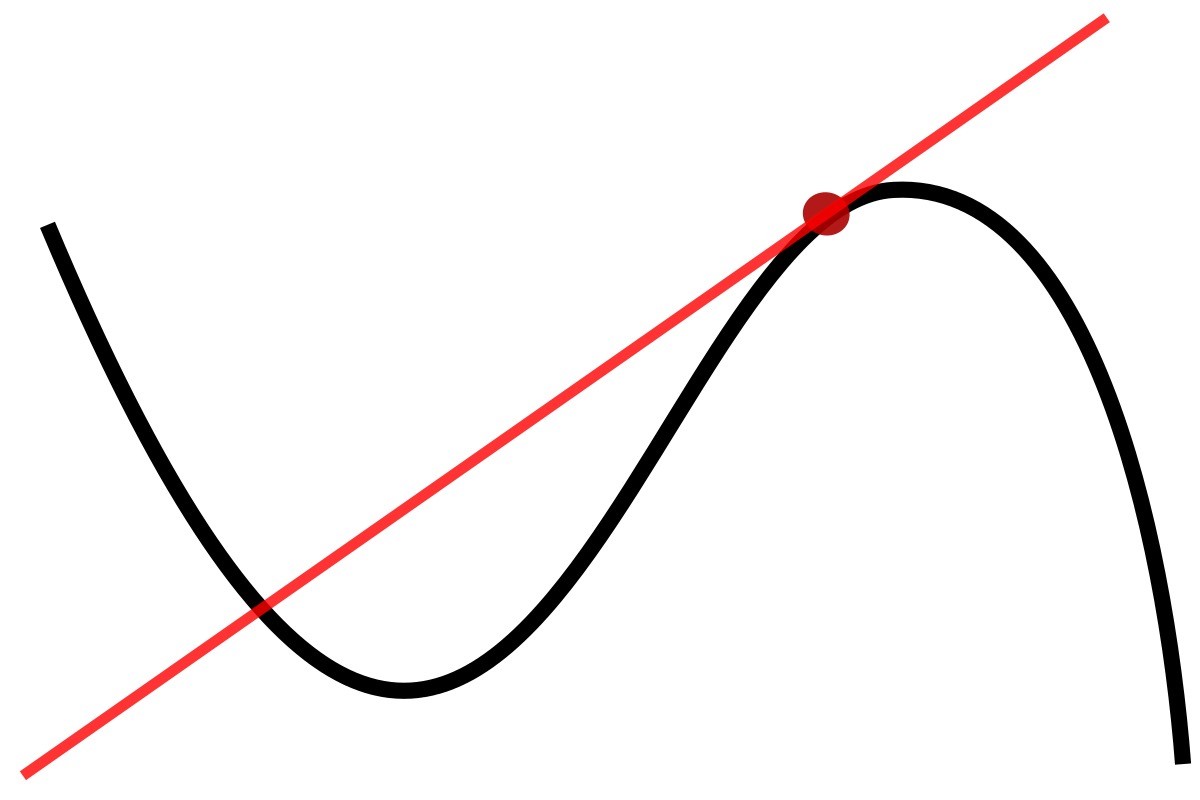
To visualize this concept, picture a curve on a graph, meandering through various peaks and valleys. At any chosen point on the curve, the tangent line touches the curve at that exact spot, mirroring its steepness. This means that the tangent line and the curve share the same slope at the point of contact. It's a brief encounter that provides a snapshot of the curve's behavior at that specific location.

Tangent lines are not bound by the constraints of the curve; they simply graze its surface at a single point, capturing the essence of its steepness without being entangled in its intricate twists and turns. This unique characteristic makes tangent lines invaluable for understanding the instantaneous rate of change of a function at a specific point. They offer a glimpse into the dynamic nature of curves, shedding light on their behavior in real-time.

In essence, understanding tangent lines involves grasping their role as emissaries of steepness, delivering crucial insights into the instantaneous rate of change of a curve at a specific point. By unraveling the mysteries of tangent lines, we gain a deeper appreciation for the dynamic nature of functions and the elegance of mathematical analysis. Now that we've uncovered the essence of tangent lines, let's delve into the art of finding their slopes and unravel the secrets they hold within the realm of calculus.

Finding the Slope of a Tangent Line

Finding the slope of a tangent line is akin to deciphering the instantaneous steepness of a curve at a specific point. This process involves unraveling the mystery of how the curve behaves at that precise location, offering a glimpse into its dynamic nature. To embark on this mathematical quest, we employ the tools of calculus, leveraging the power of derivatives to unveil the secrets held by tangent lines.

At the heart of finding the slope of a tangent line lies the concept of the derivative. The derivative of a function represents its rate of change at any given point, capturing the instantaneous slope of the curve at that location. By harnessing the derivative, we can unveil the slope of the tangent line, unlocking a wealth of information about the behavior of the curve.

To embark on this mathematical journey, we begin by selecting a point on the curve where we seek to determine the slope of the tangent line. This point serves as the epicenter of our exploration, guiding us to unravel the curve's behavior at that specific location. With the chosen point in sight, we delve into the realm of limits, a fundamental concept in calculus that enables us to capture the instantaneous rate of change.

By taking the limit as another point on the curve approaches our chosen point, we can calculate the slope of the secant line connecting these two points. As the second point converges towards the chosen point, the secant line gradually aligns with the tangent line, providing a pathway to unveil the elusive slope we seek. This process of approaching the chosen point from different directions allows us to capture the instantaneous steepness of the curve, paving the way to discover the slope of the tangent line.

Through this intricate dance of limits and convergence, we unravel the slope of the tangent line, unlocking a treasure trove of insights into the curve's behavior at that specific point. This journey of mathematical discovery equips us with the tools to comprehend the dynamic nature of functions, shedding light on their instantaneous rate of change and the elegance of mathematical analysis.

As we immerse ourselves in the art of finding the slope of a tangent line, we unravel the enigmatic nature of curves, unveiling their secrets one point at a time. This process of mathematical exploration empowers us to grasp the essence of instantaneous steepness, offering a window into the dynamic world of functions and their derivatives.

Using Calculus to Find the Slope

In the realm of calculus, the pursuit of finding the slope of a tangent line involves an intricate dance of mathematical concepts, with derivatives taking center stage in unraveling the mysteries held by curves. The derivative of a function serves as the key to unlocking the instantaneous rate of change at any given point, providing a gateway to understanding the dynamic behavior of curves.

To embark on the journey of finding the slope of a tangent line using calculus, we delve into the fundamental concept of limits. As we fix our gaze on a specific point along the curve, we harness the power of limits to capture the instantaneous behavior of the function at that precise location. By approaching the chosen point from different directions, we gain insights into the curve's behavior, paving the way to unveil the slope of the tangent line.

The process of finding the slope of a tangent line involves calculating the derivative of the function at the chosen point. This derivative represents the instantaneous rate of change of the function, encapsulating the slope of the tangent line at that specific location. Through the elegant machinery of calculus, we unravel the slope of the tangent line, shedding light on the dynamic nature of the curve at the point of contact.

By harnessing the power of derivatives and limits, we embark on a mathematical quest to capture the essence of instantaneous steepness, unveiling the secrets held by tangent lines. This journey equips us with the tools to comprehend the dynamic behavior of functions, offering a window into the intricate world of calculus and its applications in analyzing the behavior of curves.

As we immerse ourselves in the art of using calculus to find the slope of a tangent line, we unravel the enigmatic nature of curves, one derivative at a time. This process of mathematical exploration empowers us to grasp the essence of instantaneous rate of change, providing a glimpse into the dynamic world of functions and their derivatives.

Examples of Finding the Slope of a Tangent Line

Let's delve into practical examples to illuminate the process of finding the slope of a tangent line. Consider the function f(x) = x^2, a classic parabolic curve that embodies the elegance of mathematical analysis. We aim to determine the slope of the tangent line at the point where x = 2.

To initiate this mathematical exploration, we harness the power of derivatives, the cornerstone of calculus. The derivative of the function f(x) = x^2 can be calculated using the power rule, yielding f'(x) = 2x. This derivative encapsulates the instantaneous rate of change of the function at any given point.

Now, to unveil the slope of the tangent line at x = 2, we substitute the chosen x-value into the derivative. By evaluating f'(2), we obtain the slope of the tangent line at that specific point. In this case, f'(2) = 2 * 2 = 4, revealing that the slope of the tangent line to the curve f(x) = x^2 at x = 2 is 4.

Moving on to another example, let's explore the function g(x) = 3x^3 – 2x, a quintessential cubic function with its own unique characteristics. We set our sights on determining the slope of the tangent line at the point where x = 1.

Employing the power of derivatives once again, we calculate the derivative of g(x) = 3x^3 – 2x using the power rule and constant multiple rule, yielding g'(x) = 9x^2 – 2. This derivative captures the instantaneous rate of change of the function at any given point along the curve.

To unravel the slope of the tangent line at x = 1, we substitute the chosen x-value into the derivative. By evaluating g'(1), we uncover the slope of the tangent line at that specific point. Upon computation, we find that g'(1) = 9 * 1^2 – 2 = 7, indicating that the slope of the tangent line to the curve g(x) = 3x^3 – 2x at x = 1 is 7.

These examples showcase the application of derivatives in finding the slope of tangent lines, offering a glimpse into the dynamic nature of functions and the elegance of mathematical analysis. By unraveling the secrets held by tangent lines, we gain a deeper appreciation for the instantaneous rate of change and the profound insights they provide into the behavior of curves.