Home>Mathematics>How To Find Slope From A Table

Mathematics
How To Find Slope From A Table
Published: February 25, 2024
Learn how to find the slope from a table in mathematics with step-by-step instructions and examples. Master the concept of slope calculation easily.
(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)
Table of Contents
Introduction
Understanding how to find slope from a table is a fundamental concept in mathematics, particularly in the field of algebra and geometry. Slope represents the measure of the steepness of a line, and it plays a crucial role in various real-world applications, such as engineering, architecture, and physics. By learning how to calculate slope from a table, individuals can gain valuable insights into the relationship between two variables and make informed decisions based on the data presented.
In this article, we will delve into the intricacies of determining slope from a table, providing a step-by-step guide to empower readers with the knowledge and skills necessary to tackle such problems with confidence. Whether you are a student grappling with algebraic concepts or an enthusiast seeking to deepen your understanding of mathematical principles, this exploration of slope calculation from a table will equip you with practical insights and problem-solving techniques.
By the end of this article, you will have a clear grasp of the underlying principles governing slope determination and be able to apply this knowledge to analyze and interpret data presented in tabular form. Let's embark on this enlightening journey to unravel the mysteries of slope calculation and discover the profound significance of this mathematical concept in various domains.
Read more: How To Find Slope In Excel
Understanding Slope
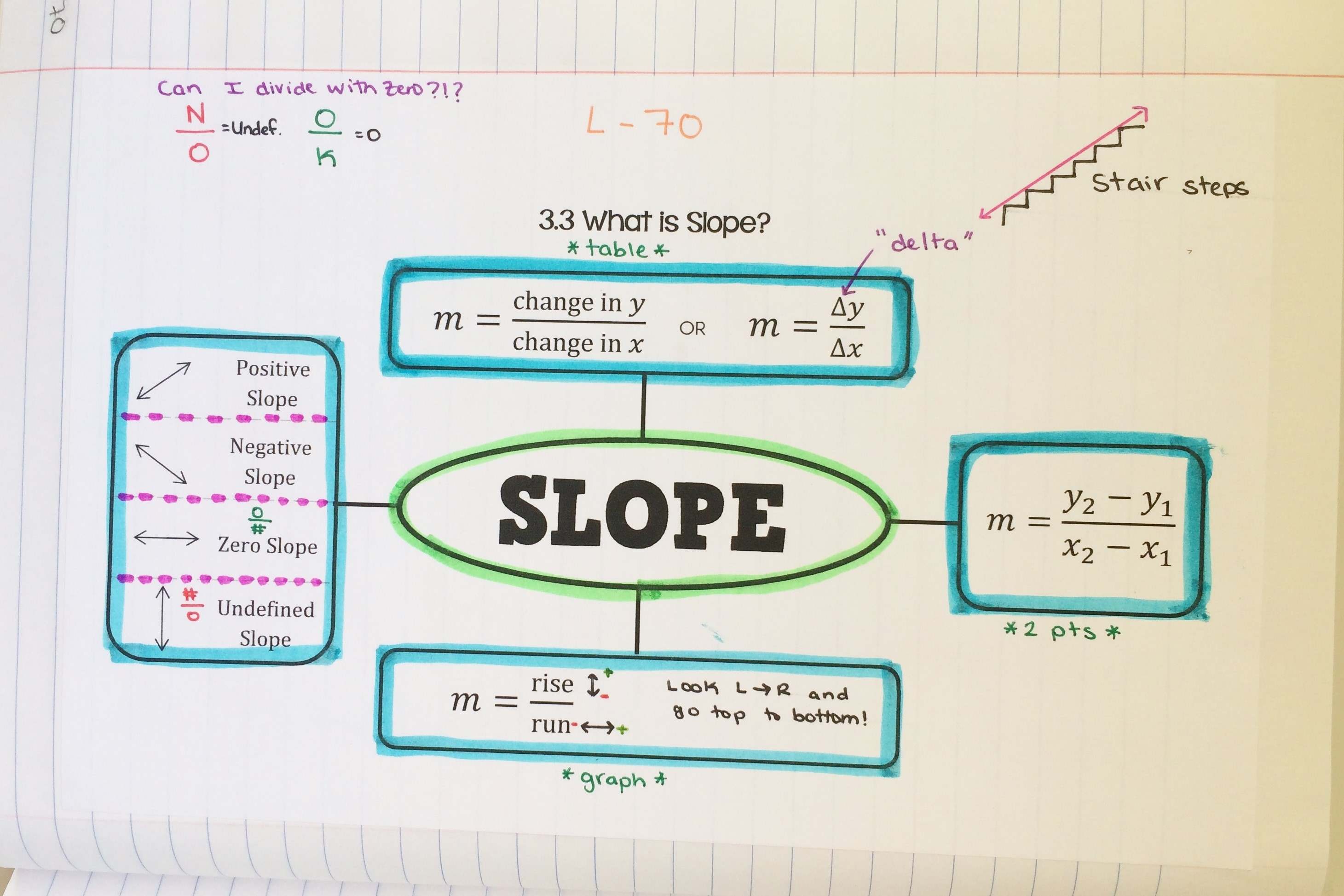
Slope is a fundamental concept in mathematics that measures the steepness of a line. It is a crucial element in understanding the relationship between two variables, often represented on a graph or in tabular form. The slope of a line indicates how much the dependent variable changes for a unit change in the independent variable. In simpler terms, it quantifies the rate at which one quantity changes concerning another.
The slope of a line can be positive, negative, zero, or undefined. A positive slope signifies an upward trend, indicating that as the independent variable increases, the dependent variable also increases. Conversely, a negative slope represents a downward trend, indicating that as the independent variable increases, the dependent variable decreases. A slope of zero indicates a horizontal line, where the dependent variable remains constant regardless of changes in the independent variable. An undefined slope occurs when dealing with vertical lines, as the independent variable remains constant while the dependent variable may vary.
In graphical representation, the slope is often visualized as the angle formed by the line with the x-axis. The steeper the line, the greater the magnitude of the slope. This visual interpretation provides an intuitive understanding of how the slope reflects the relationship between the variables.
Mathematically, the slope is calculated using the formula:
[m = frac{y_2 – y_1}{x_2 – x_1}]
where ((x_1, y_1)) and ((x_2, y_2)) are two distinct points on the line. This formula demonstrates how the change in the dependent variable ((y)) relates to the change in the independent variable ((x)), providing a precise numerical representation of the line's steepness.
Understanding slope is essential for interpreting data, making predictions, and analyzing trends. Whether in the context of economics, physics, or engineering, the concept of slope enables individuals to comprehend the underlying patterns and behaviors of variables. By mastering the intricacies of slope calculation, one gains a powerful tool for extracting valuable insights from data and making informed decisions based on the observed relationships.
Steps to Find Slope from a Table
-
Identify Data Pairs: Begin by examining the table to identify the pairs of data points. Each pair consists of values from the independent variable (often denoted as x) and the corresponding dependent variable (often denoted as y). These pairs of values represent the coordinates of points on the line, forming the basis for calculating the slope.
-
Select Two Data Points: Choose any two distinct data pairs from the table. These points will serve as the basis for calculating the slope of the line. It is essential to select points that are clearly defined in the table and represent a meaningful relationship between the variables.
-
Assign Coordinates: Label the selected data points with their respective coordinates. For instance, if the first point is represented as (x1, y1) and the second point as (x2, y2), assign these coordinates based on the values extracted from the table.
-
Calculate the Change in Y: Determine the change in the dependent variable (y) by subtracting the y-coordinate of the first point from the y-coordinate of the second point. This yields the difference in the dependent variable between the two selected points, denoted as Δy = y2 – y1.
-
Calculate the Change in X: Similarly, calculate the change in the independent variable (x) by subtracting the x-coordinate of the first point from the x-coordinate of the second point. This provides the difference in the independent variable between the two selected points, denoted as Δx = x2 – x1.
-
Compute the Slope: Utilize the formula for calculating slope, which involves dividing the change in the dependent variable by the change in the independent variable. The slope (m) is determined by the ratio of the change in y to the change in x, expressed as m = Δy / Δx.
-
Interpret the Result: Once the slope is computed, interpret its value in the context of the problem or data presented. A positive slope indicates an upward trend, a negative slope signifies a downward trend, while a slope of zero represents a horizontal line. Understanding the implications of the calculated slope enriches the analysis and facilitates a deeper comprehension of the relationship between the variables.
By following these systematic steps, individuals can effectively find the slope from a table, unraveling the underlying patterns and trends encapsulated in the data. This process equips individuals with the analytical tools to extract valuable insights and make informed decisions based on the observed relationships between variables.
Example Problem
Let's delve into an illustrative example to demonstrate the application of the steps outlined in finding the slope from a table. Consider a scenario where we have a table representing the relationship between time and distance traveled by a moving object. The table consists of the following data pairs:
| Time (hours) | Distance Traveled (miles) |
|---|---|
| 1 | 50 |
| 2 | 90 |
| 3 | 130 |
| 4 | 170 |
To determine the slope from this table, we will follow the systematic approach outlined earlier.
-
Identify Data Pairs: The table provides pairs of data, with time in hours as the independent variable (x) and the corresponding distance traveled in miles as the dependent variable (y).
-
Select Two Data Points: For this example, let's choose the data pairs (1, 50) and (3, 130) to calculate the slope.
-
Assign Coordinates: Label the selected data points with their respective coordinates: (1, 50) as (x1, y1) and (3, 130) as (x2, y2).
-
Calculate the Change in Y: The change in the dependent variable (Δy) is obtained by subtracting the y-coordinate of the first point from the y-coordinate of the second point: Δy = 130 – 50 = 80.
-
Calculate the Change in X: Similarly, the change in the independent variable (Δx) is determined by subtracting the x-coordinate of the first point from the x-coordinate of the second point: Δx = 3 – 1 = 2.
-
Compute the Slope: Applying the formula for slope calculation, we obtain the slope (m) as the ratio of the change in y to the change in x: m = Δy / Δx = 80 / 2 = 40.
By following these steps, we have successfully calculated the slope of the line representing the relationship between time and distance traveled. In this context, the slope of 40 indicates that for every one-hour increase in time, the distance traveled increases by 40 miles. This positive slope signifies a steady and consistent rate of travel, providing valuable insights into the motion of the object.
Through this example problem, we have demonstrated the practical application of finding slope from a table, showcasing how this fundamental concept enables us to interpret and analyze the relationship between variables in a real-world scenario.
Conclusion
In conclusion, the ability to find slope from a table is a valuable skill that empowers individuals to extract meaningful insights from data and comprehend the underlying relationships between variables. By following the systematic steps outlined in this article, individuals can effectively calculate the slope, thereby gaining a deeper understanding of the patterns and trends encapsulated in the tabular representation of data.
The process of finding slope from a table begins with identifying the data pairs and selecting two distinct points to serve as the basis for slope calculation. By assigning coordinates to these points and calculating the changes in the dependent and independent variables, individuals can then apply the slope formula to derive the numerical representation of the line's steepness. This calculated slope provides valuable information about the rate of change between the variables, offering crucial insights into the behavior and trends reflected in the data.
Moreover, the example problem presented in this article illustrates the practical application of finding slope from a table in a real-world scenario. By analyzing the relationship between time and distance traveled by a moving object, we demonstrated how the calculated slope enriches our understanding of the object's motion, providing valuable insights into its rate of travel.
Understanding slope is not only essential for academic pursuits but also holds practical significance in various fields, including physics, engineering, economics, and environmental science. The ability to interpret and analyze data through the lens of slope calculation equips individuals with the analytical tools to make informed decisions, predict trends, and derive meaningful conclusions from the observed relationships between variables.
In essence, the process of finding slope from a table transcends mere mathematical computation; it embodies the art of uncovering hidden patterns, making informed interpretations, and harnessing the power of data to gain valuable insights. By mastering this fundamental concept, individuals can navigate the complexities of data analysis with confidence, leveraging the principles of slope calculation to unravel the mysteries and intricacies of the relationships embedded in tabular representations.
In conclusion, the journey to find slope from a table is a transformative exploration that equips individuals with the analytical prowess to decipher the language of data, unveiling its secrets and empowering informed decision-making.