Discover The Foolproof Method To Uncover Real Zeros In A Quadratic Function!

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Quadratic functions are paramount in the realm of mathematics, playing a pivotal role in various real-world applications, from engineering and physics to economics and computer science. Understanding the behavior of quadratic functions is crucial for solving a myriad of problems, and one fundamental aspect of this understanding is the ability to uncover real zeros, which are the points where the function intersects the x-axis.

In this article, we will delve into the fascinating world of quadratic functions, exploring their characteristics and the methods to determine their real zeros. By the end of this journey, you will be equipped with a foolproof method to unveil the real zeros of a quadratic function, empowering you to tackle complex mathematical challenges with confidence.

Let's embark on this enlightening exploration, unraveling the intricacies of quadratic functions and unveiling the secrets to uncovering their real zeros. So, fasten your seatbelt and get ready to delve into the captivating realm of quadratic functions!

Understanding Quadratic Functions

Quadratic functions are a fundamental concept in algebra, defined by the equation f(x) = ax^2 + bx + c, where a, b, and c are constants, and a is not equal to 0. These functions are graphically represented by a parabola, a U-shaped curve, which can open upwards or downwards based on the value of 'a'. The leading coefficient 'a' determines the direction and width of the parabola, while the constants 'b' and 'c' influence its position on the coordinate plane.

The graph of a quadratic function is symmetric about its axis of symmetry, which is a vertical line passing through the vertex of the parabola. This vertex represents the minimum or maximum point of the function, depending on whether the parabola opens upwards or downwards. Understanding the properties of the vertex, axis of symmetry, and direction of the parabola is essential for comprehending the behavior of quadratic functions.

Moreover, quadratic functions are characterized by their concavity, which refers to the curvature of the parabola. If the parabola opens upwards, the function is said to be concave up, while a parabola opening downwards indicates a concave down function. This concavity plays a crucial role in determining critical points, inflection points, and the overall shape of the graph.

Furthermore, quadratic functions are widely utilized to model various real-world phenomena, such as projectile motion, financial analysis, and optimization problems. Their ability to accurately represent and analyze complex relationships makes them indispensable in fields ranging from physics and engineering to economics and biology.

In summary, understanding quadratic functions involves grasping their graphical representation, key features such as the vertex and axis of symmetry, and their significance in modeling real-world scenarios. This foundational knowledge serves as a springboard for exploring the methods to uncover real zeros of quadratic functions, which we will delve into in the subsequent sections.

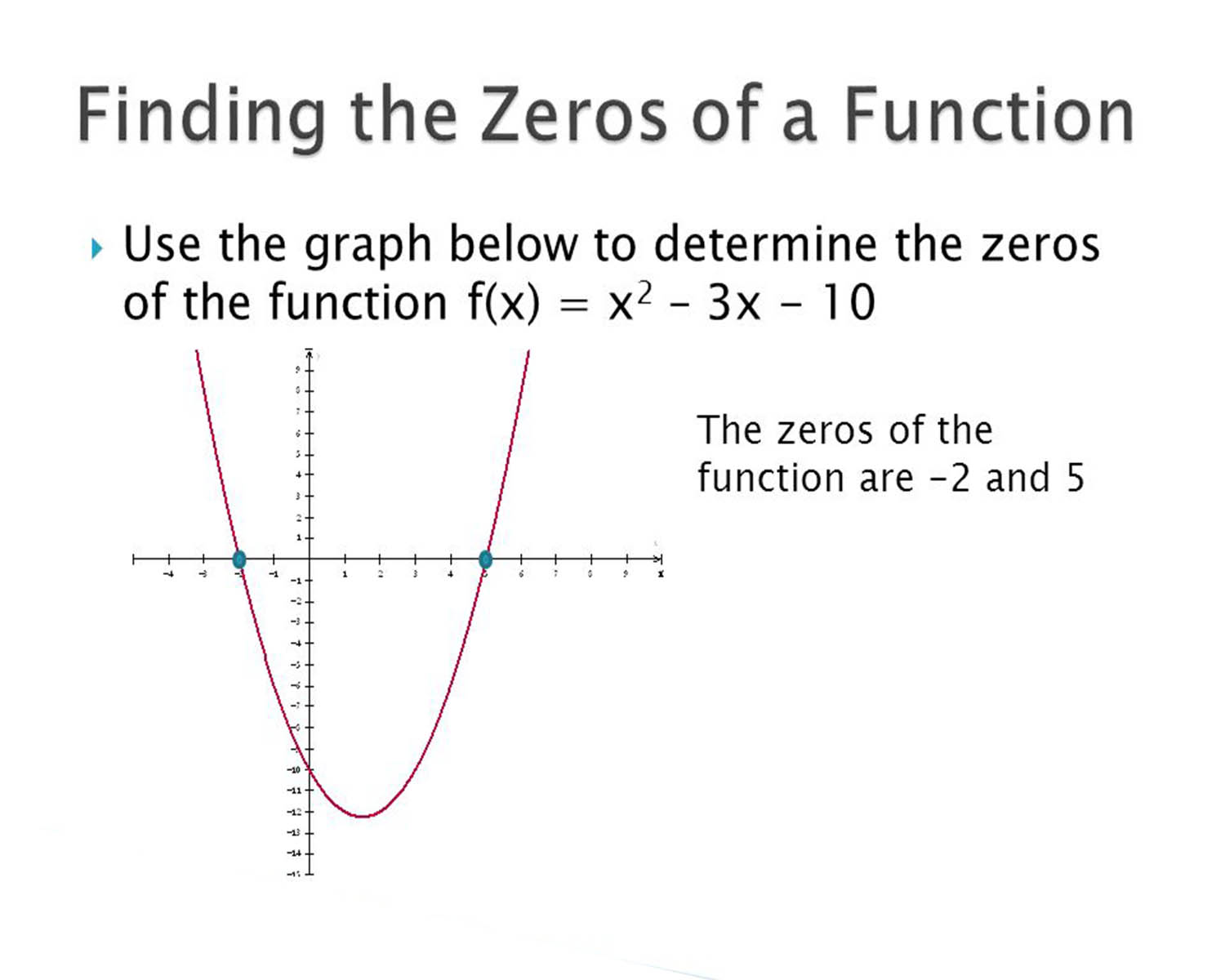
Finding Zeros of Quadratic Functions

In the realm of quadratic functions, uncovering the zeros holds immense significance, as these points mark the locations where the function intersects the x-axis. These zeros, also known as roots or solutions, provide crucial insights into the behavior of the quadratic function and are pivotal in various applications, including solving equations, analyzing motion, and optimizing processes.

The process of finding the zeros of a quadratic function involves determining the values of 'x' for which the function equals zero. Mathematically, this translates to solving the quadratic equation ax^2 + bx + c = 0. The solutions to this equation represent the x-coordinates of the points where the quadratic function crosses the x-axis.

To find the zeros, one commonly employed method is the quadratic formula, which provides a straightforward and systematic approach to solving quadratic equations. The quadratic formula states that for a quadratic equation of the form ax^2 + bx + c = 0, the solutions for 'x' are given by:

x = (-b ± √(b^2 – 4ac)) / (2a)

This elegant formula encapsulates the essence of the quadratic equation, offering a direct means to compute the zeros of the quadratic function. By substituting the coefficients 'a', 'b', and 'c' into the quadratic formula, one can efficiently determine the real or complex roots of the quadratic equation.

Moreover, the graphical interpretation of finding zeros involves identifying the x-intercepts of the parabolic curve representing the quadratic function. These x-intercepts correspond to the points where the function intersects the x-axis, signifying the values of 'x' at which the function evaluates to zero. Graphically visualizing the zeros provides an intuitive understanding of their significance in relation to the shape and behavior of the quadratic function.

Furthermore, the discriminant, denoted by Δ = b^2 – 4ac, plays a pivotal role in determining the nature of the roots. If the discriminant is positive, the quadratic equation has two distinct real roots, indicating that the parabola intersects the x-axis at two distinct points. When the discriminant is zero, the equation possesses a single real root, implying that the parabola touches the x-axis at a single point. Conversely, if the discriminant is negative, the roots are complex, indicating that the parabola does not intersect the x-axis in the real number domain.

In essence, the process of finding zeros of quadratic functions encompasses both algebraic and graphical methods, offering a comprehensive approach to unraveling the solutions of quadratic equations. This fundamental skill forms the bedrock for the foolproof method to uncover real zeros, which we will explore in the subsequent section.

The Foolproof Method to Uncover Real Zeros

When it comes to uncovering the real zeros of a quadratic function with absolute certainty, the foolproof method lies in leveraging the concept of factoring. This method, rooted in the fundamental theorem of algebra, provides a systematic approach to determining the real roots of a quadratic equation, offering unparalleled clarity and precision in the process.

The essence of the factoring method revolves around transforming the quadratic equation into a product of linear factors, thereby unveiling the values of 'x' at which the function equals zero. This transformative process enables a direct and intuitive interpretation of the roots, shedding light on the precise points of intersection between the quadratic function and the x-axis.

The key to implementing the factoring method lies in recognizing the quadratic equation in its standard form, ax^2 + bx + c = 0, and subsequently factoring it into the form (px + q)(rx + s) = 0, where p, q, r, and s are constants. By factoring the quadratic equation in this manner, the solutions for 'x' can be readily identified by setting each linear factor equal to zero and solving for 'x', yielding the real zeros of the quadratic function.

Moreover, the factoring method offers profound insights into the behavior of the quadratic function, as it unveils the factors that contribute to the formation of the parabolic curve. By discerning the linear factors and their corresponding roots, one gains a comprehensive understanding of how the quadratic function intersects the x-axis, elucidating the intricate relationship between the equation and its graphical representation.

Furthermore, the factoring method seamlessly integrates with the graphical interpretation of quadratic functions, as it elucidates the process of identifying the x-intercepts of the parabola. This cohesive synergy between algebraic manipulation and graphical analysis empowers individuals to grasp the essence of real zeros in a holistic manner, bridging the gap between abstract equations and tangible geometric representations.

In essence, the foolproof method to uncover real zeros through factoring encapsulates the elegance and efficacy of algebraic techniques, providing a robust framework for unraveling the solutions of quadratic equations with precision and clarity. By harnessing the power of factoring, individuals can confidently navigate the intricate landscape of quadratic functions, unlocking the secrets to their real zeros with unwavering certainty.

Conclusion

In conclusion, the journey through the realm of quadratic functions has been nothing short of enlightening and empowering. We've traversed the intricate landscape of quadratic equations, unraveling their graphical representations, understanding their key features, and delving into the methods to uncover their real zeros. Through this exploration, we've gained a profound appreciation for the elegance and significance of quadratic functions in both theoretical and practical domains.

The process of finding real zeros of quadratic functions is not merely a mathematical exercise; it is a gateway to unlocking profound insights into the behavior of these functions. Whether employing the quadratic formula, leveraging the factoring method, or interpreting the graphical manifestations, the quest for real zeros offers a captivating journey into the heart of quadratic equations.

Furthermore, the foolproof method of factoring has emerged as a beacon of certainty in the pursuit of real zeros. Its seamless integration of algebraic manipulation and graphical interpretation provides a comprehensive understanding of the roots of quadratic functions, bridging the gap between abstract equations and tangible geometric representations.

As we conclude this exploration, it is evident that the ability to uncover real zeros in a quadratic function is not merely a mathematical skill; it is a gateway to unraveling the intricate relationships between algebraic expressions and their graphical manifestations. This proficiency holds immense value in diverse fields, from engineering and physics to finance and computer science, where quadratic functions serve as indispensable tools for modeling and analysis.

In essence, the journey to uncover real zeros in quadratic functions transcends the realm of mathematics, offering a profound glimpse into the interconnectedness of mathematical concepts and their real-world applications. Armed with the foolproof method to uncover real zeros, we stand poised to navigate the complexities of quadratic functions with confidence and precision, equipped with the knowledge to unravel their secrets and harness their power in diverse problem-solving scenarios.

So, as we bid adieu to this captivating exploration, let us carry forth this newfound understanding, embracing the elegance and significance of quadratic functions, and the timeless allure of uncovering their real zeros.

This is just the beginning of a journey filled with endless possibilities, where the beauty and depth of mathematics intertwine with the practical intricacies of our world, shaping our understanding and empowering us to conquer new frontiers with unwavering certainty and boundless curiosity.