Home>Mathematics>How To Use The Square Root Symbol
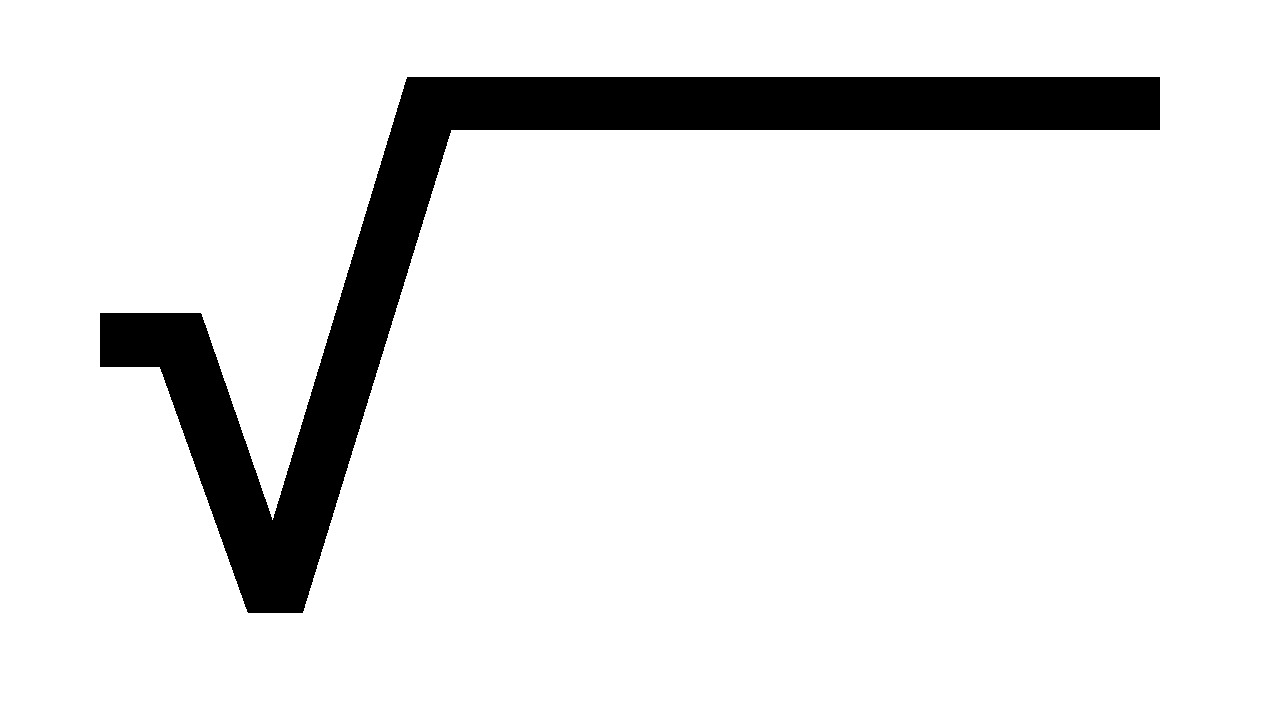
Mathematics
How To Use The Square Root Symbol
Published: February 26, 2024
Learn how to use the square root symbol in mathematics with our step-by-step guide. Master the basics of mathematical notation and operations.
(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)
Table of Contents
Introduction
The square root symbol is a fundamental element in mathematics, representing the inverse operation of squaring a number. It holds a significant place in various mathematical concepts, including algebra, geometry, and calculus. Understanding how to use the square root symbol is essential for solving equations, analyzing data, and comprehending complex mathematical principles.
In this article, we will delve into the intricacies of the square root symbol, exploring its significance, practical applications, and methods for typing it on a computer. Whether you are a student grappling with mathematical concepts or a professional seeking to enhance your understanding of mathematical notation, this guide will equip you with the knowledge and skills to effectively utilize the square root symbol in your mathematical endeavors.
Let's embark on a journey to unravel the mysteries of the square root symbol, demystifying its complexities and discovering its practical implications in the realm of mathematics. By the end of this article, you will gain a comprehensive understanding of how to wield this symbol with confidence and precision, empowering you to tackle mathematical challenges with ease and proficiency.
Understanding the Square Root Symbol
The square root symbol, denoted by the radical sign (√), is a fundamental mathematical notation that represents the principal square root of a number. When applied to a non-negative real number, the square root yields a value that, when multiplied by itself, equals the original number. This concept is pivotal in mathematics, serving as a cornerstone for various mathematical principles and real-world applications.
The square root symbol is derived from the radical symbol used in ancient mathematics, signifying the extraction of roots. Its modern representation as the radical sign (√) was introduced in the 16th century, providing a concise and standardized notation for denoting square roots.
In mathematical terms, the square root of a number x is denoted as √x, where the radical sign (√) indicates the operation of finding the non-negative square root of x. It is important to note that the square root of a negative number is considered a complex number and is denoted using the imaginary unit "i."
Understanding the properties and characteristics of the square root symbol is essential for comprehending its role in mathematical equations, functions, and geometric concepts. The square root operation is intrinsically linked to the concept of squares and serves as a foundational element in the study of quadratic equations, geometric shapes, and numerical analysis.
Moreover, the square root symbol embodies the concept of inverse operations, as it reverses the effect of squaring a number. This inverse relationship between squaring and taking the square root underpins the symmetry and balance inherent in mathematical operations, facilitating the manipulation and analysis of numerical data and mathematical expressions.
By grasping the essence of the square root symbol, individuals can unlock a deeper understanding of mathematical relationships, enabling them to solve equations, analyze geometric properties, and interpret numerical data with precision and insight. The versatility and ubiquity of the square root symbol underscore its significance as a fundamental building block of mathematical reasoning and problem-solving.
In the subsequent sections, we will explore the practical methods for typing the square root symbol on a computer and delve into its applications in mathematical equations and real-world scenarios. This journey will illuminate the diverse facets of the square root symbol, empowering readers to harness its potential in their mathematical pursuits.
Typing the Square Root Symbol on a Computer
Typing the square root symbol (√) on a computer is a straightforward process that enables users to incorporate mathematical notation into digital documents, presentations, and online platforms. Whether you are creating a mathematical equation, drafting a technical report, or designing educational materials, the ability to input the square root symbol is essential for accurately conveying mathematical concepts in a digital format.
There are several methods for typing the square root symbol on a computer, catering to different operating systems and software applications. One of the most common approaches involves utilizing keyboard shortcuts to insert the square root symbol seamlessly. For Windows users, the shortcut involves pressing "Alt" + "251" on the numeric keypad, while Mac users can use the combination "Option" + "V" to insert the symbol into their documents.
In addition to keyboard shortcuts, many word processing and mathematical software programs offer dedicated tools for inserting mathematical symbols, including the square root symbol. For instance, Microsoft Word provides an "Equation Editor" feature that allows users to access a comprehensive library of mathematical symbols and notation, including the square root symbol, for effortless integration into documents.
Furthermore, LaTeX, a typesetting system widely used for technical and scientific documents, offers a specialized command (sqrt{}) for representing the square root symbol within mathematical expressions. This versatile approach enables users to create complex mathematical equations and formulas with precision and clarity, making it a preferred choice for researchers, academics, and professionals in technical fields.
Moreover, the Unicode standard, which governs the encoding and representation of text in digital systems, includes the square root symbol as a designated character (U+221A). This standardized encoding ensures the consistent display and interpretation of the square root symbol across different platforms and devices, facilitating seamless communication of mathematical content in digital environments.
By leveraging these methods and tools, individuals can effortlessly incorporate the square root symbol into their digital documents and mathematical expressions, enhancing the clarity and professionalism of their work. Whether it's a scientific research paper, a mathematical presentation, or an educational resource, the ability to type the square root symbol on a computer empowers users to communicate complex mathematical concepts effectively in the digital realm.
In the subsequent sections, we will explore the practical applications of the square root symbol in mathematical equations and real-world scenarios, shedding light on its significance in diverse fields and problem-solving contexts. This exploration will illuminate the versatility and impact of the square root symbol, showcasing its relevance in both theoretical and practical domains.
Using the Square Root Symbol in Mathematical Equations
The square root symbol plays a pivotal role in mathematical equations, offering a powerful tool for solving problems across various domains of mathematics. When incorporated into equations, the square root symbol enables mathematicians, scientists, and engineers to manipulate and analyze numerical relationships, uncovering valuable insights and solutions. Its application extends to diverse mathematical disciplines, including algebra, calculus, and physics, where the extraction of square roots is integral to formulating and solving complex equations.
In algebraic equations, the square root symbol is employed to solve quadratic equations, which are fundamental in modeling real-world phenomena and optimizing mathematical functions. By utilizing the square root symbol, mathematicians can determine the roots of quadratic equations, providing critical information about the behavior and properties of mathematical functions. This process is essential for identifying critical points, determining the nature of solutions, and analyzing the geometric characteristics of parabolic curves, which are prevalent in physics, engineering, and optimization problems.
Furthermore, the square root symbol is instrumental in expressing mathematical relationships and constraints in various scientific and engineering contexts. For instance, in physics and engineering, the square root symbol is utilized to calculate the magnitude of vectors, representing physical quantities such as velocity, acceleration, and force. By incorporating the square root symbol into vector equations, scientists and engineers can accurately determine the magnitude of vector quantities, facilitating the analysis and prediction of physical phenomena in diverse fields, including mechanics, electromagnetism, and fluid dynamics.
In the realm of calculus, the square root symbol features prominently in the context of integration and differential equations, where it is utilized to represent the solutions to differential equations and the integration of functions involving square roots. This application underscores the significance of the square root symbol in facilitating the analysis of dynamic systems, population dynamics, and physical processes governed by differential equations, providing a powerful framework for modeling and understanding complex phenomena in natural and engineered systems.
Moreover, the square root symbol is integral to statistical analysis and data interpretation, where it is employed to calculate standard deviations, variance, and measures of uncertainty in datasets. By leveraging the square root symbol, statisticians and data analysts can quantify the dispersion and variability of data, enabling informed decision-making and rigorous analysis in fields such as finance, economics, and social sciences.
In essence, the square root symbol serves as a versatile and indispensable tool in mathematical equations, empowering practitioners across diverse disciplines to solve problems, model phenomena, and extract meaningful insights from numerical data. Its pervasive presence in mathematical expressions and equations underscores its relevance and impact in theoretical and applied mathematics, highlighting its enduring significance as a fundamental element of mathematical reasoning and problem-solving.
Practical Applications of the Square Root Symbol
The practical applications of the square root symbol extend across a myriad of fields, encompassing scientific, engineering, financial, and technological domains. Its versatile utility transcends theoretical mathematics, finding resonance in real-world scenarios where precise measurements, calculations, and analyses are paramount. By harnessing the power of the square root symbol, professionals and researchers can unravel complex phenomena, optimize systems, and make informed decisions in diverse contexts.
In engineering and physics, the square root symbol is instrumental in determining the magnitude of physical quantities, such as velocity, acceleration, and force. By calculating the square root of the sum of squared components of a vector, engineers and physicists can ascertain the magnitude of a vector, providing crucial insights into the intensity and direction of physical quantities in mechanical, electrical, and aerospace systems. This application is pivotal in designing efficient propulsion systems, analyzing structural loads, and optimizing the performance of complex engineering systems.
Moreover, the square root symbol plays a pivotal role in financial modeling and risk analysis, particularly in the calculation of standard deviation and volatility. In the realm of finance, the square root symbol is employed to compute the standard deviation of asset returns, enabling investors and analysts to assess the variability and risk associated with investment portfolios. This application facilitates the quantification of market volatility, guiding investment strategies, and risk management decisions in the dynamic landscape of financial markets.
In the realm of computer science and digital communication, the square root symbol is utilized in algorithms and cryptographic protocols, contributing to the security and efficiency of digital systems. For instance, in cryptographic algorithms such as RSA (Rivest-Shamir-Adleman), the square root modulo a prime number is employed as a fundamental operation in encryption and decryption processes, safeguarding sensitive information and enabling secure communication in digital environments. This application underscores the indispensable role of the square root symbol in ensuring the integrity and confidentiality of digital data and communications.
Furthermore, the square root symbol finds practical relevance in geometric and spatial analysis, where it is utilized to calculate distances, areas, and geometric properties of shapes and structures. In fields such as architecture, urban planning, and geographic information systems (GIS), the square root symbol enables professionals to quantify spatial relationships, optimize layouts, and assess the spatial distribution of resources, contributing to the design and management of sustainable built environments.
In essence, the practical applications of the square root symbol permeate diverse disciplines, offering a powerful framework for quantitative analysis, optimization, and decision-making. Its ubiquitous presence in scientific, engineering, financial, and technological domains underscores its enduring significance as a fundamental tool for unraveling complexities, modeling phenomena, and driving innovation in the modern world.
Conclusion
In conclusion, the square root symbol stands as a timeless emblem of mathematical reasoning and problem-solving, permeating diverse realms of human endeavor with its profound implications and practical utility. From its ancient origins as a symbol of root extraction to its modern-day applications in scientific research, engineering design, financial analysis, and digital communication, the square root symbol embodies the enduring legacy of mathematical innovation and empirical inquiry.
As we have journeyed through the intricacies of the square root symbol, we have unraveled its significance as a fundamental building block of mathematical reasoning, enabling us to comprehend the symmetries of nature, quantify the uncertainties of data, and optimize the complexities of human-made systems. Its presence in algebraic equations, geometric analysis, statistical inference, and cryptographic algorithms underscores its versatility and indispensability in diverse domains, empowering practitioners to unravel mysteries, model phenomena, and make informed decisions in a world shaped by mathematical principles.
Moreover, our exploration of the square root symbol has illuminated its role as a unifying force in the pursuit of knowledge, transcending disciplinary boundaries and cultural divides to offer a universal language of precision and clarity. Whether in the elegant curves of a parabolic trajectory, the intricate patterns of encrypted data, or the dynamic interplay of physical forces, the square root symbol serves as a beacon of insight and understanding, guiding us through the complexities of the natural world and the intricacies of human ingenuity.
As we embrace the timeless legacy of the square root symbol, let us recognize its enduring relevance in our quest for knowledge, innovation, and progress. By harnessing its power to unravel mysteries, model phenomena, and make informed decisions, we honor the legacy of mathematical inquiry and empirical discovery, perpetuating the timeless tradition of human intellect and ingenuity.
In the grand tapestry of human achievement, the square root symbol stands as a testament to the enduring power of mathematical reasoning, inspiring generations to unravel the mysteries of the universe, optimize the complexities of human systems, and embrace the timeless pursuit of knowledge and understanding.