The Ultimate Guide To Finding The Apothem Of A Regular Polygon

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Welcome to the ultimate guide to finding the apothem of a regular polygon! Whether you're a student delving into the fascinating world of geometry or a professional seeking to apply mathematical concepts in real-life scenarios, understanding the apothem of a regular polygon is a fundamental skill. In this comprehensive guide, we will unravel the intricacies of regular polygons and demystify the concept of apothem, equipping you with the knowledge and tools to calculate this essential geometric element with confidence.

Regular polygons are geometric figures with sides of equal length and angles of equal measure. From the familiar equilateral triangle to the complex dodecagon, these polygons exhibit symmetrical beauty and possess unique properties that are essential to comprehend in various mathematical and practical contexts. As we embark on this journey, we will explore the inherent characteristics of regular polygons, laying the groundwork for a deeper understanding of their apothems.

The concept of apothem is integral to the study of regular polygons, offering insights into their internal structure and facilitating calculations related to area, perimeter, and other geometric properties. Understanding the apothem empowers us to analyze and manipulate regular polygons with precision, making it a vital component of geometric problem-solving and mathematical exploration.

Throughout this guide, we will delve into the formulas and methodologies for calculating the apothem of a regular polygon, providing step-by-step instructions and practical examples to illustrate its application in real-world scenarios. By the end of our journey, you will possess a comprehensive understanding of the apothem, enabling you to navigate the intricate world of regular polygons with confidence and proficiency.

So, fasten your mathematical seatbelt and prepare to embark on an enlightening exploration of regular polygons and the enigmatic apothem. Whether you're a math enthusiast, a student preparing for exams, or a professional seeking to apply geometric principles in your field, this guide will equip you with the knowledge and skills to master the art of finding the apothem of a regular polygon. Let's dive in and unravel the mysteries of geometry together!

Understanding Regular Polygons

Regular polygons are geometric figures characterized by the uniformity of their sides and angles. These symmetrical shapes possess a captivating allure, from the simplicity of the equilateral triangle to the intricacy of the dodecagon. At the core of their allure lies a fundamental principle: the equality of their internal components.

In a regular polygon, each side is of equal length, and each angle is of equal measure, endowing these geometric entities with a harmonious balance that transcends their individual complexities. This uniformity gives rise to a sense of symmetry and order, making regular polygons a subject of fascination for mathematicians, artists, and enthusiasts alike.

The defining feature of a regular polygon is its ability to tessellate, or tile, a plane without leaving any gaps or overlaps. This unique property underpins the visual appeal and structural integrity of regular polygons, making them invaluable in various design and architectural contexts.

From the timeless elegance of the equilateral triangle to the multifaceted allure of the dodecagon, regular polygons manifest in a myriad of forms, each with its distinct set of properties and characteristics. As we delve into their world, we encounter the captivating interplay of geometry and symmetry, unraveling the intricate patterns and relationships that define these geometric marvels.

Regular polygons serve as the building blocks of geometric exploration, providing a framework for understanding fundamental concepts such as area, perimeter, and interior angles. Their symmetrical nature facilitates precise calculations and geometric constructions, making them indispensable tools in mathematical problem-solving and creative endeavors.

By comprehending the inherent properties of regular polygons, we gain insights into the foundational principles of geometry, paving the way for deeper explorations into their diverse applications. From architectural designs to artistic compositions, the symmetrical allure of regular polygons continues to inspire and captivate, underscoring their enduring relevance in the realms of mathematics and beyond.

What is an Apothem?

An apothem is a fundamental geometric element that holds a pivotal role in the realm of regular polygons. Specifically, it refers to a line segment drawn from the center of a regular polygon to the midpoint of any side, forming a right angle with that side. This perpendicular distance from the center to a side showcases the intrinsic relationship between the polygon's symmetry and its internal structure.

The apothem serves as a crucial determinant of a regular polygon's characteristics, offering valuable insights into its area, perimeter, and other geometric properties. By understanding the apothem, mathematicians and enthusiasts can unravel the symmetrical intricacies of regular polygons, unlocking the key to precise calculations and geometric analyses.

In essence, the apothem embodies the harmony and balance inherent in regular polygons, encapsulating the geometric precision and uniformity that define these captivating shapes. Its significance extends beyond mere measurement, as it provides a gateway to deeper explorations of symmetry, tessellation, and the fundamental principles of geometry.

From the majestic simplicity of the equilateral triangle to the multifaceted allure of the dodecagon, the apothem serves as a unifying element, bridging the geometric intricacies of regular polygons with the foundational principles of mathematics. Its presence enriches our understanding of symmetry, angles, and spatial relationships, fostering a deeper appreciation for the elegant precision that underpins the world of geometry.

As we delve into the world of regular polygons and their apothems, we embark on a journey of discovery, unraveling the timeless allure of symmetry and precision. The apothem stands as a testament to the intrinsic beauty and structural integrity of regular polygons, inviting us to explore their captivating properties and unlock the secrets held within their symmetrical embrace.

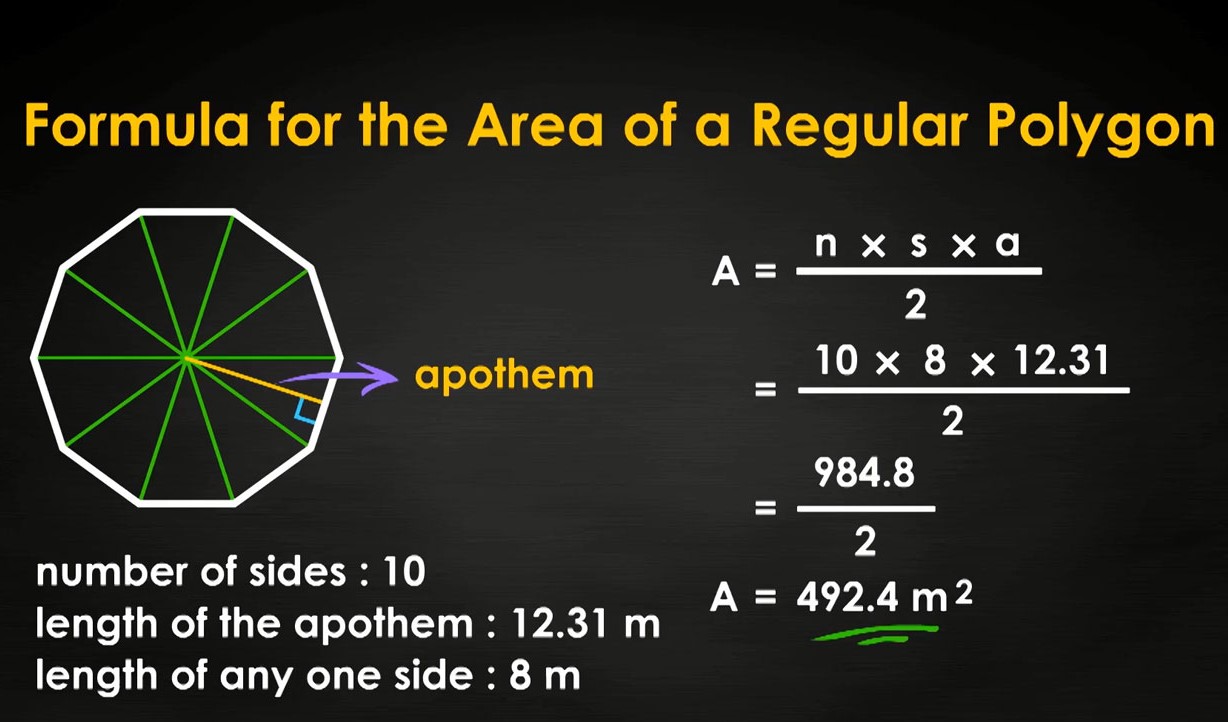
Formulas for Calculating Apothem

In the realm of geometry, the calculation of the apothem for a regular polygon is facilitated by specific formulas tailored to capture the essence of its symmetrical structure. The apothem serves as a crucial element in determining the area and perimeter of regular polygons, making the understanding of its calculation formulas essential for geometric analyses and problem-solving.

For a regular polygon with side length 's' and the number of sides 'n', the formula for calculating the apothem is given by:

[ text{Apothem} = frac{s}{2 times tan(frac{pi}{n})} ]

This formula encapsulates the relationship between the side length, the number of sides, and the tangent function, providing a precise method for determining the apothem of a regular polygon. By leveraging this formula, mathematicians and enthusiasts can unravel the symmetrical intricacies of regular polygons, unlocking the key to precise calculations and geometric analyses.

In addition to the tangent-based formula, the apothem of a regular polygon can also be calculated using the radius of the inscribed circle, denoted as 'r'. The relationship between the apothem and the radius of the inscribed circle is defined by the following formula:

[ text{Apothem} = r times cos(frac{pi}{n}) ]

This alternative formula offers a complementary approach to calculating the apothem, providing mathematicians and students with a versatile toolkit for exploring the geometric properties of regular polygons. By understanding and applying these formulas, individuals can delve into the symmetrical allure of regular polygons, gaining insights into their internal structure and geometric precision.

These formulas for calculating the apothem of a regular polygon serve as foundational tools in the realm of geometry, enabling precise measurements and geometric analyses. By mastering these formulas, mathematicians and enthusiasts can navigate the intricate world of regular polygons with confidence, unraveling the mysteries of symmetry and precision that underpin their geometric allure.

Step-by-Step Guide to Finding the Apothem

1. Identify the Regular Polygon: Begin by identifying the regular polygon for which you intend to calculate the apothem. Note the number of sides, denoted as 'n', and the length of each side, denoted as 's'. Understanding the specific characteristics of the regular polygon is essential for accurate apothem calculation.

2. Select the Calculation Method: Choose the appropriate method for calculating the apothem based on the available information. You can opt to utilize the tangent-based formula, which involves the side length and the number of sides, or the formula based on the radius of the inscribed circle, leveraging the relationship between the apothem and the circle's radius.

3. Implement the Tangent-Based Formula: If utilizing the tangent-based formula, apply the following steps:

   • Calculate the angle: Determine the value of the angle by dividing π (pi) by the number of sides, denoted as 'n'.
   • Compute the tangent: Find the tangent of the calculated angle.
   • Calculate the apothem: Divide the side length 's' by 2 times the tangent of the angle to obtain the apothem of the regular polygon.

4. Utilize the Inscribed Circle Radius Formula: If opting for the formula based on the radius of the inscribed circle, proceed as follows:

   • Determine the radius: Calculate the radius of the inscribed circle, denoted as 'r', by dividing the side length 's' by 2 times the tangent of π divided by the number of sides, 'n'.
   • Compute the apothem: Multiply the radius of the inscribed circle by the cosine of π divided by the number of sides, 'n', to obtain the apothem of the regular polygon.

5. Verify the Calculation: After obtaining the apothem using the chosen method, verify the result to ensure accuracy. Cross-check the calculations and, if feasible, compare the apothem obtained from both the tangent-based and inscribed circle radius formulas to validate the accuracy of the calculated value.

6. Apply the Apothem in Geometric Analyses: Once the apothem is accurately calculated, leverage its value in various geometric analyses and problem-solving scenarios. Explore its significance in determining the area, perimeter, and other geometric properties of the regular polygon, showcasing the practical applications of the calculated apothem.

By following this step-by-step guide, you can confidently navigate the process of finding the apothem of a regular polygon, leveraging precise calculations and geometric methodologies to unravel the symmetrical intricacies of these geometric marvels.

Practical Examples

To illustrate the practical application of finding the apothem of a regular polygon, let's delve into real-world scenarios where this geometric element plays a crucial role.

Architectural Design:

Imagine you are an architect tasked with designing a building facade adorned with a captivating geometric pattern. The design concept revolves around incorporating a series of regular polygons, each with a distinct apothem, to create a visually striking and mathematically precise arrangement. By calculating the apothems of the polygons, you can ensure uniformity in the dimensions and spatial relationships, resulting in an aesthetically pleasing and harmonious architectural composition.

Tiling Patterns:

In the realm of interior design and decorative tiling, the concept of regular polygons and their apothems holds significant relevance. Consider a project where a space is adorned with intricate tiling patterns featuring various regular polygons, such as hexagons and octagons. By calculating the apothems of these polygons, designers can ensure seamless tessellation and precise alignment, resulting in visually captivating and structurally sound tiling arrangements.

Engineering and Construction:

In the field of engineering and construction, the apothem of a regular polygon finds practical utility in diverse applications. For instance, in the design and construction of structural elements such as trusses and frames, the precise calculation of apothems facilitates the determination of load-bearing capacities and geometric stability. By leveraging the apothem measurements, engineers can optimize the structural integrity of geometric components, ensuring safety and efficiency in construction projects.

Artistic Installations:

Artists and sculptors often integrate geometric elements, including regular polygons and their apothems, into their creative works. Imagine a large-scale artistic installation featuring a series of regular polygons arranged in a symmetrical and visually captivating configuration. By calculating the apothems of these polygons, artists can ensure precise dimensions and spatial relationships, resulting in an evocative and mathematically inspired artistic masterpiece.

Geometric Landscaping:

In the realm of landscape design and urban planning, the concept of regular polygons and their apothems influences the creation of geometrically themed outdoor spaces. Consider a public park adorned with geometrically shaped pathways and garden beds featuring regular polygons. By calculating the apothems of these polygons, landscape architects can achieve geometric precision and spatial harmony, enhancing the visual appeal and structural coherence of the outdoor environment.

In each of these practical examples, the calculation of the apothem of a regular polygon serves as a foundational step in achieving geometric precision, spatial harmony, and visual allure. By applying the principles of geometry to real-world scenarios, individuals across diverse fields harness the intrinsic beauty and mathematical elegance of regular polygons and their apothems, shaping environments and creations that resonate with precision and aesthetic sophistication.

Conclusion

In the realm of geometry, the exploration of regular polygons and their apothems unveils a captivating tapestry of symmetry, precision, and practical significance. Throughout this comprehensive guide, we have embarked on a journey of discovery, unraveling the enigmatic allure of regular polygons and delving into the fundamental principles of finding their apothems. As we conclude our exploration, it is evident that the apothem serves as a gateway to understanding the profound symmetrical intricacies and practical applications of regular polygons.

The significance of the apothem extends far beyond its role as a geometric measurement. It embodies the harmonious balance and structural integrity of regular polygons, encapsulating the essence of symmetry and precision that underpin the world of geometry. By mastering the art of finding the apothem, mathematicians, students, and professionals alike gain access to a versatile toolkit for precise calculations, geometric analyses, and real-world applications.

From architectural design to artistic installations, engineering to interior decor, the practical examples showcased the pervasive influence of regular polygons and their apothems across diverse fields. The calculated apothem serves as a linchpin in achieving geometric precision, spatial harmony, and visual allure, shaping environments and creations that resonate with mathematical elegance and aesthetic sophistication.

As we reflect on our journey, it becomes evident that the apothem of a regular polygon embodies the timeless allure of symmetry and the intrinsic beauty of geometric precision. Its calculations and applications offer a gateway to deeper explorations of spatial relationships, tessellation, and the foundational principles of geometry. By unraveling the mysteries of regular polygons and their apothems, we gain insights into the elegant symmetries that underpin the fabric of our geometric world.

In conclusion, the quest to find the apothem of a regular polygon transcends mere mathematical calculations; it embodies a profound exploration of symmetry, precision, and practical relevance. As we apply the principles of geometry to real-world scenarios, we harness the intrinsic beauty and mathematical elegance of regular polygons and their apothems, shaping environments and creations that resonate with precision and aesthetic sophistication. Let the symmetrical allure of regular polygons and their apothems continue to inspire and captivate, underscoring their enduring relevance in the realms of mathematics and beyond.