How To Divide Decimals

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Noodls.com, at no extra cost. Learn more)

Introduction

Welcome to the fascinating world of decimal division! Whether you're a student tackling this concept for the first time or an adult refreshing your math skills, understanding how to divide decimals is a valuable skill with real-world applications. From calculating precise measurements to managing finances, mastering decimal division opens doors to a multitude of practical uses.

In this comprehensive guide, we will delve into the intricacies of dividing decimals, providing you with a step-by-step approach, valuable tips, and common pitfalls to avoid. By the end of this journey, you will feel confident in your ability to tackle decimal division problems with ease and precision.

So, why is understanding decimal division so important? Decimals are an essential part of our everyday lives, appearing in various contexts such as money, measurements, and scientific calculations. Being able to divide decimals accurately empowers you to make precise calculations in these areas, ensuring that you can confidently manage tasks ranging from splitting a restaurant bill to calculating the exact dimensions of a room for a home improvement project.

Moreover, mastering decimal division lays a solid foundation for more advanced mathematical concepts. As you progress in your mathematical journey, you will encounter scenarios where a strong grasp of decimal division is crucial for solving complex problems. By building a solid understanding of this fundamental skill, you are setting yourself up for success in more advanced math courses and future endeavors.

Throughout this guide, we will explore the principles of decimal division in a clear and approachable manner, breaking down complex concepts into manageable steps. Whether you're a visual learner who benefits from practical examples or someone who thrives on understanding the underlying principles, this guide is designed to cater to various learning styles, ensuring that you can grasp the concepts at your own pace.

So, without further ado, let's embark on this enlightening journey into the world of decimal division, where we will unravel the mysteries and master the art of dividing decimals with confidence and precision.

Understanding Decimal Division

Decimal division involves dividing numbers that include decimal points. It is a fundamental mathematical operation that allows us to make precise calculations in various real-world scenarios. Understanding decimal division requires a solid grasp of the relationship between decimals and whole numbers, as well as the principles of place value.

When we divide decimals, we are essentially breaking down a quantity into equal parts, just like in whole number division. However, the presence of decimal points adds an extra layer of complexity. To comprehend decimal division, it's crucial to recognize the significance of the decimal point in relation to the numbers being divided.

In decimal division, the placement of the decimal point is crucial in determining the accuracy of the quotient. The number of decimal places in the dividend and divisor directly impacts the placement of the decimal point in the quotient. Understanding how to align the decimal points correctly is essential for obtaining accurate results in decimal division.

Moreover, it's important to recognize that dividing decimals is akin to multiplying both the dividend and divisor by powers of 10 to eliminate the decimal points. This concept is foundational to understanding why the placement of the decimal point in the quotient is determined by the total number of decimal places in the dividend and divisor.

Furthermore, understanding decimal division involves recognizing the relationship between fractions and decimals. Decimal division can be viewed as a way to convert fractions to decimals and vice versa. This connection underscores the importance of decimal division as a tool for working with fractional quantities in a decimal format.

By grasping these fundamental principles, you will develop a solid foundation for tackling decimal division with confidence. As we delve deeper into the step-by-step guide to dividing decimals, these underlying concepts will serve as the building blocks for mastering this essential mathematical skill.

Understanding decimal division is not just about manipulating numbers; it's about developing a deeper appreciation for the interconnectedness of mathematical concepts and their practical applications. With this understanding, you are well-equipped to navigate the intricacies of decimal division and harness its power in solving real-world problems with precision and accuracy.

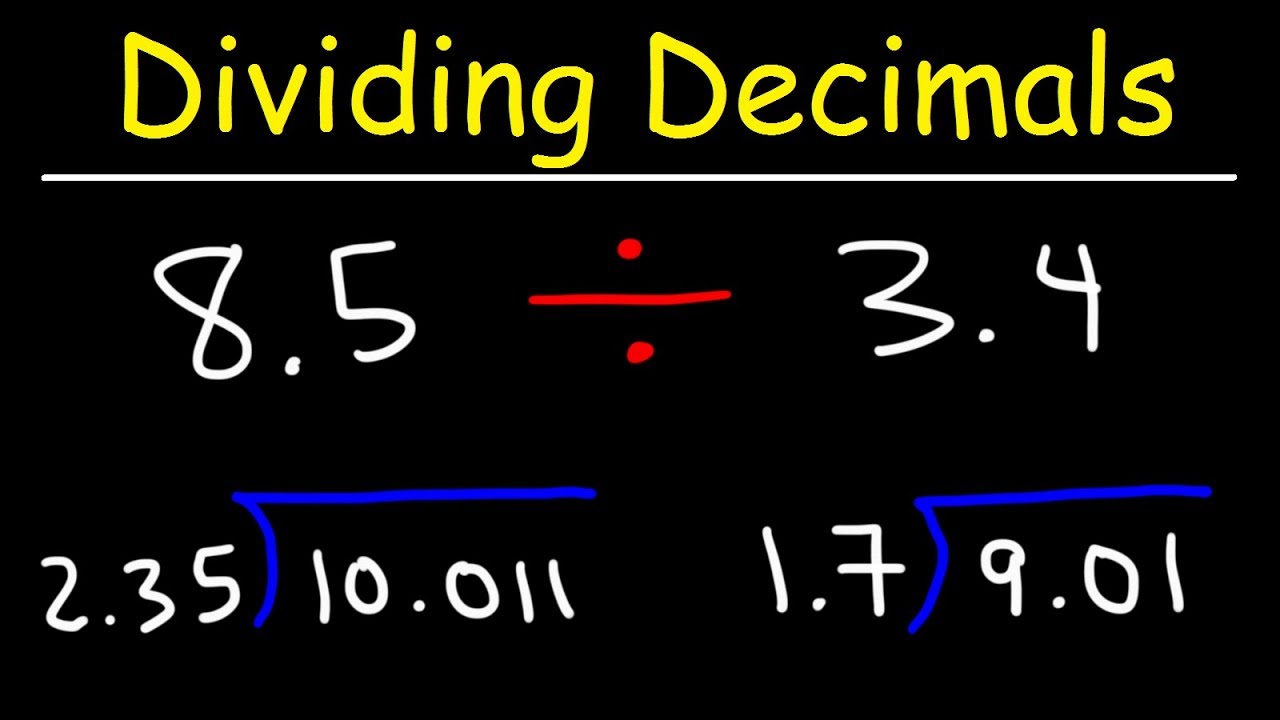
Step-by-Step Guide to Dividing Decimals

Dividing decimals may seem daunting at first, but with a systematic approach, you can confidently tackle any decimal division problem. Let's explore a step-by-step guide to dividing decimals, breaking down the process into manageable and intuitive steps.

1. Align the Decimal Points: Begin by aligning the decimal points in the dividend and divisor. This ensures that the numbers are properly positioned for the division process. If the divisor is not a whole number, you can add zeros to the end of it to make it a whole number without altering its value.

2. Convert to Whole Numbers: To simplify the division process, you can convert the decimal divisor into a whole number by moving the decimal point to the right. Simultaneously, move the decimal point in the dividend by the same number of places to maintain the equivalence of the numbers being divided.

3. Perform the Division: Once the divisor is a whole number, proceed with the division as you would with whole numbers. Divide the modified dividend by the whole number divisor, just as you would in long division.

4. Adjust the Decimal Point: After obtaining the quotient from the division of the modified numbers, it's time to reintroduce the decimal point. The placement of the decimal point in the quotient is determined by the total number of decimal places in the original dividend and divisor. Count the total decimal places in the original numbers and position the decimal point in the quotient accordingly.

5. Check for Precision: It's crucial to verify the precision of the quotient by considering the context of the problem. If you're dealing with measurements or financial calculations, ensure that the decimal point is correctly placed to reflect the appropriate level of precision.

6. Practice and Refine: The key to mastering decimal division lies in practice. Work through a variety of problems to reinforce your understanding and refine your skills. As you encounter different scenarios, you'll become adept at recognizing patterns and applying the step-by-step process with ease.

By following this systematic guide, you can confidently navigate the intricacies of dividing decimals, empowering yourself to make precise calculations in a wide range of real-world situations. With practice and perseverance, you'll develop a strong command of decimal division, unlocking the potential to solve complex problems with accuracy and confidence.

Tips and Tricks for Dividing Decimals

When it comes to dividing decimals, mastering the fundamental principles is essential, but having a few tips and tricks up your sleeve can significantly enhance your efficiency and accuracy. Here are some valuable strategies to streamline the decimal division process and overcome common challenges:

1. Clear Alignment:

Ensure that the decimal points in the dividend and divisor are perfectly aligned before commencing the division. This alignment sets the stage for a smooth and accurate division process, preventing errors in the placement of the decimal point in the quotient.

2. Power of Estimation:

Embrace the power of estimation to gauge the approximate magnitude of the quotient. By rounding the dividend and divisor to the nearest whole numbers, you can quickly estimate the rough value of the quotient, providing a helpful reference point for the actual division.

3. Utilize Multiplication:

In some cases, it may be more intuitive to convert the divisor into a whole number by multiplying both the divisor and dividend by a power of 10. This transformation simplifies the division process, making it easier to work with whole numbers before reintroducing the decimal point in the final quotient.

4. Contextual Precision:

Consider the context of the problem to determine the appropriate level of precision for the quotient. If you're dealing with measurements or financial calculations, ensure that the decimal point in the quotient accurately reflects the desired level of precision, aligning with the specific requirements of the scenario.

5. Remain Consistent:

Maintain consistency in the number of decimal places throughout the division process. Whether aligning the decimal points, converting to whole numbers, or reintroducing the decimal point in the quotient, consistency ensures accuracy and coherence in the final result.

6. Practice with Real-World Scenarios:

Engage in practical exercises that mirror real-world situations, such as dividing measurements or currency values. By applying decimal division to authentic scenarios, you'll develop a practical understanding of its applications and refine your skills in a contextually relevant manner.

By incorporating these tips and tricks into your approach to dividing decimals, you can streamline the process, enhance precision, and build confidence in your ability to tackle decimal division problems with finesse. These strategies serve as valuable tools in your mathematical arsenal, empowering you to navigate the complexities of decimal division with ease and proficiency.

Common Mistakes to Avoid

As you embark on your journey to master decimal division, it's crucial to be mindful of common pitfalls that can lead to errors and misconceptions. By recognizing and understanding these potential stumbling blocks, you can proactively steer clear of them, ensuring that your decimal division endeavors yield accurate and reliable results. Let's explore some of the most prevalent mistakes to avoid when dividing decimals:

1. Misaligned Decimal Points:

One of the most frequent errors in decimal division occurs when the decimal points in the dividend and divisor are not correctly aligned. This misalignment can lead to inaccuracies in the placement of the decimal point in the quotient, resulting in erroneous results. To avoid this mistake, always double-check the alignment of decimal points before commencing the division process.

2. Inconsistent Treatment of Decimal Places:

Maintaining consistency in the number of decimal places throughout the division process is paramount. Failing to adhere to a consistent approach when aligning decimal points, converting to whole numbers, and reintroducing the decimal point in the quotient can introduce errors and inconsistencies in the final result. By ensuring uniformity in handling decimal places, you can mitigate the risk of miscalculations.

3. Neglecting Contextual Precision:

A common oversight in decimal division involves overlooking the contextual precision required for the quotient. Depending on the nature of the problem, such as dealing with measurements or financial values, it's essential to consider the appropriate level of precision for the quotient. Neglecting to align the decimal point with the specific precision requirements of the scenario can lead to inaccuracies in the final result.

4. Skipping Verification of Quotient Precision:

After obtaining the quotient in decimal division, it's crucial to verify the precision of the result in relation to the context of the problem. Failing to double-check the placement of the decimal point in the quotient can result in an imprecise or misleading answer. Always take the time to ensure that the decimal point accurately reflects the desired level of precision for the given scenario.

5. Overlooking the Relationship with Fractions:

Decimal division is closely linked to the concept of fractions, and overlooking this relationship can hinder a comprehensive understanding of the division process. Recognizing the equivalence between fractions and decimals is essential for grasping the underlying principles of decimal division. By acknowledging this connection, you can approach decimal division with a more holistic perspective, enhancing your overall proficiency.

By being mindful of these common mistakes and actively avoiding them, you can fortify your foundation in decimal division, paving the way for accurate and confident problem-solving. As you navigate the intricacies of dividing decimals, vigilance against these pitfalls will empower you to approach each problem with precision and clarity, ultimately leading to mastery in this essential mathematical skill.

Practice Problems

Now that we've explored the fundamental principles, step-by-step guide, and valuable tips for dividing decimals, it's time to put your skills to the test with a series of practice problems. Engaging with these problems will not only reinforce your understanding of decimal division but also provide an opportunity to apply the concepts in diverse scenarios. As you work through these practice problems, remember to align the decimal points, maintain precision, and consider the context of each scenario to ensure accurate results.

Problem 1:

Divide 5.4 by 0.6. Align the decimal points and determine the quotient, ensuring the appropriate level of precision for the result.

Problem 2:

A recipe calls for 1.75 cups of flour, and you need to make 3 batches. How much flour, in cups, will you need in total? Divide the total amount of flour required by the number of batches to find the quantity needed for each batch.

Problem 3:

You have a budget of $450 for a home improvement project. If you plan to allocate 30% of the budget to painting, how much money, in dollars, will be dedicated to painting? Divide the total budget by the percentage to determine the amount allocated for painting.

Problem 4:

A rectangular garden measures 8.2 meters in length and 3.5 meters in width. What is the area of the garden in square meters? Divide the product of the length and width to find the area of the garden.

Problem 5:

You have 6.3 feet of ribbon, and you want to cut it into pieces that are 0.9 feet long. How many pieces of ribbon can you cut? Divide the total length of ribbon by the length of each piece to determine the number of pieces.

Problem 6:

A car travels 124.8 miles on 4.8 gallons of fuel. What is the car's mileage in miles per gallon (MPG)? Divide the distance traveled by the amount of fuel consumed to calculate the car's mileage.

By working through these practice problems, you'll gain hands-on experience in applying decimal division to practical scenarios, ranging from measurements and recipes to budgeting and fuel efficiency. As you tackle each problem, pay attention to the precision of your results and consider the real-world implications of the solutions. With practice and perseverance, you'll sharpen your skills in dividing decimals, equipping yourself with the confidence and proficiency to tackle a wide array of decimal division problems with ease.

Conclusion

In conclusion, mastering the art of dividing decimals is a valuable skill with far-reaching implications in both academic and real-world contexts. Throughout this comprehensive guide, we have navigated the intricacies of decimal division, unraveling its fundamental principles, providing a step-by-step guide, offering valuable tips and tricks, highlighting common mistakes to avoid, and engaging in practical problem-solving. As we reflect on this journey, it becomes evident that decimal division is not merely a mathematical concept but a practical tool that empowers us to make precise calculations in diverse scenarios.

By understanding the relationship between decimals and whole numbers, recognizing the significance of decimal point alignment, and appreciating the contextual precision required for the quotient, we have laid a solid foundation for confidently approaching decimal division problems. The step-by-step guide has equipped us with a systematic approach to dividing decimals, emphasizing the importance of clear alignment, whole number conversion, and precision verification. Additionally, the valuable tips and tricks presented have provided us with strategic tools to streamline the division process and enhance our efficiency and accuracy.

Moreover, by acknowledging common mistakes and actively avoiding them, we have fortified our understanding of decimal division, ensuring that our problem-solving endeavors yield accurate and reliable results. Engaging with practice problems has allowed us to apply the concepts in diverse scenarios, reinforcing our proficiency in dividing decimals and honing our skills in a contextually relevant manner.

As we conclude this exploration of decimal division, it's important to recognize the broader significance of this skill. From managing finances and calculating measurements to solving real-world problems, the ability to divide decimals accurately opens doors to a multitude of practical applications. Furthermore, mastering decimal division lays a solid foundation for more advanced mathematical concepts, setting the stage for success in academic pursuits and future endeavors.

In essence, the journey into the world of decimal division has not only equipped us with a valuable mathematical skill but has also fostered a deeper appreciation for the interconnectedness of mathematical concepts and their practical applications. With a solid understanding of decimal division, we are well-prepared to navigate the complexities of real-world scenarios, making precise calculations with confidence and accuracy. As we continue to refine our skills through practice and perseverance, we embrace the transformative power of decimal division in shaping our mathematical proficiency and problem-solving capabilities.